In this assignment, we are going to implement a handful of common functional building blocks using our Scheme interpreter. We will then use those building blocks to solve a simple problem.

The functions we will be writing all involve recursion, so lets review how to write a recursive function. We will use the factorial function as an example:

First, we need to establish a base case, or the set of conditions under which we can stop recursively calling the function, and return a result. For the factorial function, this is the case when n $=0.$ When we reach the condition n $=0,$ we know that we can stop recursively calling the factorial function, and just return the value $1.$

$($define fact $($lambda $($n$)($if $(=$ n $0)1...)))$

Next, we need to establish our recursive case. To implement the recursive case, we use a simpler version of our problem, and assume that we have a function that is capable of solving that simpler version. It is important that this simpler version of our problem gets us closer to our base case.

For our n factorial problem, our recursive case involves the simpler problem of finding $($n $-1)!$ and then multiplying the result by n$.$ Note that for any positive value of n$,$ subtracting one from n will get us closer to our base case of n $=0.$

We assume the existence of a function $($simple$\_$fact$)$ capable of solving the simpler version of our problem:

$($define fact $($lambda $($n$)($if $(=$ n $0)1(*($simple$\_$fact $(-$ n $1))$ n$))))$ Finally, we replace the call to simple$\_$fact with a call to fact, and we have our implementation:

$($define fact $($lambda $($n$)($if $(=$ n $0)1(*($fact $(-$ n $1))$ n$))))$

You should follow these same steps for the functions we will be writing in Scheme in this assignment.

text file called core.scm to yresources directory. We will use this file to store the definitions of our new Scheme functions.

Finally, you need to add the tests for this assignment. On Brightspace, attached to this assignment, you will find a file named Integration$06$Test.java. Download this file and copy it into your local repository$$s src$/$test$/$java$/$ca$/$dal$/$csci$3137$ directory. Then commit and push the updates to GitLab.

Now you should be ready to begin tackling this assignment.

The Assignment

In this assignment, we are going to write subroutines in Scheme, and have our interpreter load those subroutines when it starts up$,$ so that they will be available in the REPL just like the procedures we wrote in the last three assignments. We will then use those subroutines to solve a simple problem.

Update the REPL

The first step in this assignment is to update the Main class to load the contents of core.scm so that any subroutines defined there can be available in our read$-$evaluate$-$print loop. If you look in the testEval function of the Integration$06$Test class, you will find an easy way to load this file upon startup. Simply load the entire file as a String, tokenize it$.$ Parse the resulting sequence of tokens into abstract syntax trees, and evaluate them. Be sure to hold on to the referencing environment between evaluations since we expect those evaluations to add new definitions.

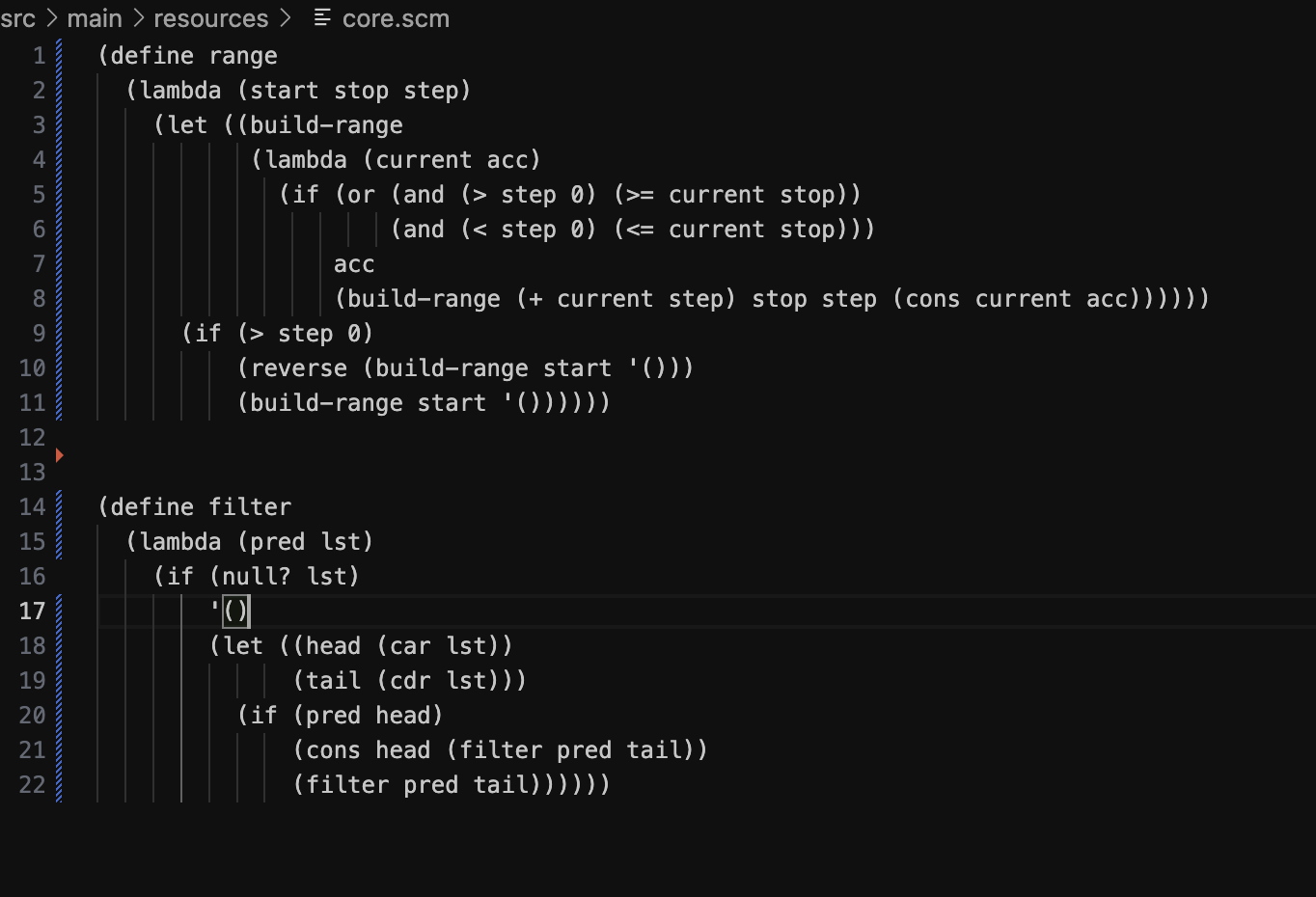
The range Function $(1$ mark$)$

The range function accepts three integer arguments: start, stop, step and returns a list containing all the integers from start $($inclusive$)$ and stop $($exclusive$)$ incrementing by step. $($You can assume that the step argument will never be zero.$)$

$>($range $1101)$

$(123456789)>($range $1203)$

$(14710131619)>($range $21201)()$

$>($range $10-10-5)(1050-5)$

The filter Function

$(1$ mark$)$

The filter function accepts two arguments; the first is a predicate and the second is a list. The filter function applies the predicate to each element of the list, and returns the sub$-$list of elements for which the predicate returns true.

$>($filter list? $\text{'}($no $($yes$)1()))$

$(($Symbol$\{$name$=$'yes'$\})())$

$($r$>($filter $($lambda $($x$)$ #t$)\text{'}($the quick brown fox$))($Symbol$\{$name$=$'the'$\}$ Symbol$\{$name$=$'quick'$\}$ Symbol$\{$name$=$'brown'$\}$ Symbol$\{$name$=$'fox'$\})$

$>($filter $($lambda $($x$)$ #f$)\text{'}($jumps over the lazy dog$))$

$()$

$>($filter $($lambda $($x$)$ x$)\text{'}(1$ z #f #t$)))$

MY MAIN CLASS IS WORKING well. The problem is adding functions and the reverse isn't working in core.scm $1($define range $($let $(($build$-$range $($if $($or $($and $(>$ step $0)(>=$ current stop$))$ acc $($if $(>$ step $0)($build$-$range start $\text{'}())))))$

$($define filter $($if $($null$?$ lst$)($let $(($head $($car lst$))($if $($pred head$)($filter pred tail$))))))\}$ BigInteger nextValue $=$ current.add$($step$)$;$\}$

$\}$;

Procedure REVERSE $=$ new Procedure$()\{$public Object apply$($Pair arguments, Map OUTPUT DEBUG CONSOLE TERMINALat org.junit.platform.engine.support.hierarchical.Throwabl

eCollector.execute$($ThrowableCollector$.$java:$73)$

at org.junit.platform.engine.support.hierarchical.NodeTest