In this code challenge, we will implement a linear regression model. The code structure we provide can be used to multivariate linear regression, where the target variable has multiple variables (outdim>1), or we can simply assume (outdim=1) in this code challenge.

 

Single-Variate Linear Regression

Remember in single-variate linear regression, the closed-form solution is given as

where in our case,

are the feature matrix and the target vector, respectively.

 

Multi-Variate Linear Regression

In the case of multivariate linear regression, we have to predict instead of a single target variable, a target vector that is comprised of multiple variables. But don't worry, doing multivariate linear regression is equivalent to doing single-variate linear regression independently multiple times. In other words, we can make a single-variate regression for the first dimension of the target vector, and for the second, until the last dimension.

How can we demonstrate this in the language of mathematics? Suppose the input feature matrix is defined as in the case of single-variate linear regression, and all the target vectors comprise the target matrix:

where indim denotes the number of the dimension of the input data, and outdim denotes the number of the dimension of the target vector. Luckily, the closed-form solution to the Multi-Variate Linear Regression looks exactly the same as the case we covered during the lecture!

Now it's your job to implement this multi-variate linear regression!

Instruction

Here is a list of the functions you need to implement:

LinearReg.fit(X, T): fit the data, learn the parameter matrix W. Available unit test: TestFit

LinearReg.predict(X): predict the target vector using the learned parameter matrix W. Available unit test: TestPredict

Here is a short example of how this LinearReg is used in the real-world application:

where we first a LinearReg object, then fit it to the training data, and calculate its loss value for the training data and the test data.

Some tips:

Use Numpy library for this homework.

np.hstack() for matrix a..>@/.matmul()/.dot() for matrix multiplication in Numpy.

np.linalg.inv() for matrix inverse computation.

Some important notes:

Read through the annotations in the .py file.

Whenever there's a pass statement, you will have to implement the code.

The implementation is auto-graded in the lesson, make sure you mark (bottom-right corner) your implementation before the deadline.

You can try multiple times until you manage to get all the credits.

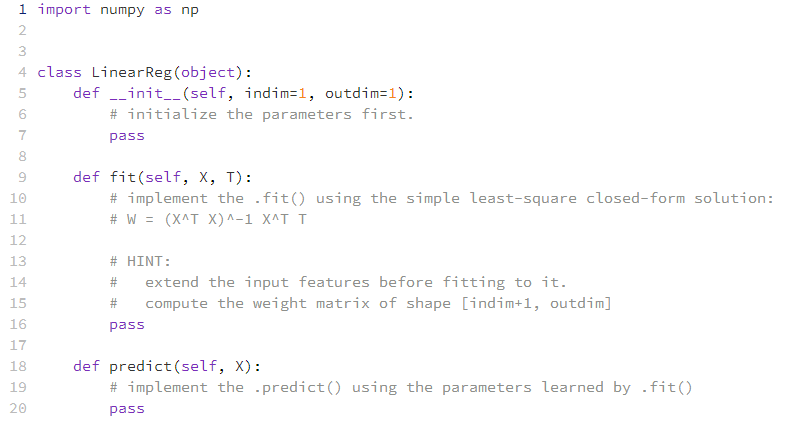
1 import numpy as np 2 3 4 class LinearReg(object): 5 6 7 8 00 9 10 11 12 13 14 15 16 17 18 19 20 def __init__(self, indim=1, outdim=1): # initialize the parameters first. pass def fit (self, X, T): # implement the .fit() using the simple least-square closed-form solution: # W = (X^T X)^-1 X^T T # HINT: # extend the input features before fitting to it. # compute the weight matrix of shape [indim+1, outdim] pass def predict(self, X): # implement the predict() using the parameters learned by .fit() pass