In this code i need to change the variables for calculating Delta and Vega using the likelihood ratio method for Asian option, because the current formulas in the code below are not correct and gives dimensional error. Note: Please don't use AI to solve this problem.

The formulas that should be used are:

Delta:

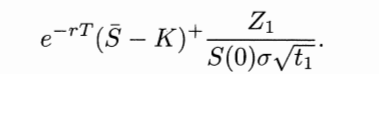Vega:

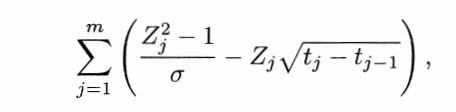
The code provided is the following:

import numpy as np import pandas as pd from IPython.display import Markdown, display

S0 = 100 K = np.array([80, 100, 120]).reshape(1, 3) r = 0.03 sigma = 0.2 T = 1 m = np.array([12, 52]) number_of_sim = 20000 h = np.array([1, 0.01]) dt = 1 / m

time_step = {0: np.arange(dt[0], T + dt[0], dt[0]).reshape(1, m[0])} S = {0: np.zeros((number_of_sim, m[0]))} Z = {0: np.random.standard_normal((number_of_sim, m[0]))} delta = {0: np.zeros((1, 3))} vega = {0: np.zeros((1, 3))}

for i in range(1, 2): time_step[i] = np.arange(dt[i], T + dt[i], dt[i]).reshape(1, m[1]) Z[i] = np.random.standard_normal((number_of_sim, m[i])) S[i] = np.zeros((number_of_sim, m[i])) delta[i] = np.zeros((1, 3)) vega[i] = np.zeros((1, 3))

for i in range(2): S[i][:, 0] = S0 * np.exp((r - 0.5 * sigma**2) * dt[i] + np.sqrt(dt[i]) * sigma * Z[i][:, 0])

for i in range(2): for j in range(m[i] - 1): S[i][:, j + 1] = S[i][:, j] * np.exp((r - 0.5 * sigma**2) * dt[i] + np.sqrt(dt[i]) * sigma * Z[i][:, j + 1])

# Calculate mean_S for each case (m=12 and m=52) mean_S = {0: np.mean(S[0], axis=1).reshape(number_of_sim, 1), 1: np.mean(S[1], axis=1).reshape(number_of_sim, 1)}

# Initialize Delta and Vega dictionaries for both cases delta = {0: np.zeros((1, 3)), 1: np.zeros((1, 3)} vega = {0: np.zeros((1, 3)), 1: np.zeros((1, 3)}

for i in range(2): # Calculate Delta using the likelihood ratio method delta[i] = np.exp(-r * T) * (mean_S[i] > K) * (Z[i][:, -1] / (S0 * sigma * np.sqrt(T / m[i]))) # Calculate Vega using the likelihood ratio method vega[i] = np.exp(-r * T) * (mean_S[i] > K) * np.sum((Z[i]**2 - 1) / sigma - Z[i] * np.sqrt(time_step[i][0, 1:]), axis=1) / S0

strikes = ['K = 80', 'K = 100', 'K = 120']

df = pd.DataFrame(index=['Delta (LRM)', 'Vega (LRM)'], columns=strikes)

for i in range(3): df.loc['Delta (LRM)', strikes[i]] = round(delta[0][i], 3) df.loc['Vega (LRM)', strikes[i]] = round(vega[0][i], 3)

display(Markdown("#### Asian call m = 12")) display(df)

df2 = pd.DataFrame(index=['Delta (LRM)', 'Vega (LRM)'], columns=strikes)

for i in range(3): df2.loc['Delta (LRM)', strikes[i]] = round(delta[1][i], 3) df2.loc('Vega (LRM)', strikes[i]] = round(vega[1][i], 3)

display(Markdown("#### Asian call m = 52")) display(df2)

erT(SK)+S(0)t1Z1 j=1m(Zj21Zjtjtj1) erT(SK)+S(0)t1Z1 j=1m(Zj21Zjtjtj1)