Question
in this code the equation is hard coded i want this code to be change in like user can give any kind of equation. (Additional
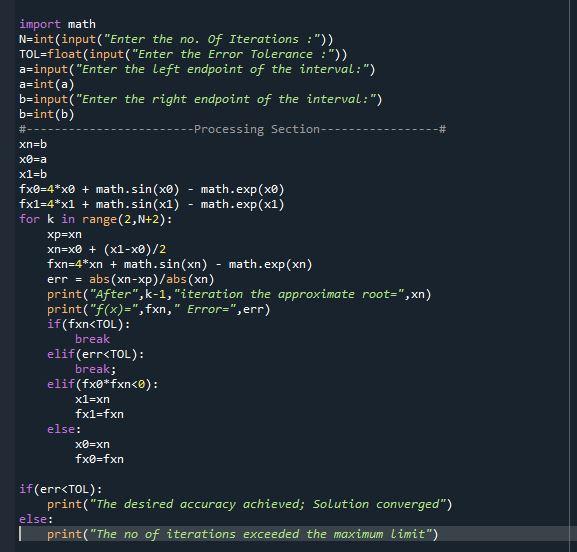
in this code the equation is hard coded i want this code to be change in like user can give any kind of equation.
(Additional info this is the code of bisection method) written form of code:
import math N=int(input("Enter the no. Of Iterations :")) TOL=float(input("Enter the Error Tolerance :")) a=input("Enter the left endpoint of the interval:") a=int(a) b=input("Enter the right endpoint of the interval:") b=int(b) #------------------------Processing Section-----------------# xn=b x0=a x1=b fx0=4*x0 + math.sin(x0) - math.exp(x0) fx1=4*x1 + math.sin(x1) - math.exp(x1) for k in range(2,N+2): xp=xn xn=x0 + (x1-x0)/2 fxn=4*xn + math.sin(xn) - math.exp(xn) err = abs(xn-xp)/abs(xn) print("After",k-1,"iteration the approximate root=",xn) print("f(x)=",fxn," Error=",err) if(fxn if(err
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


