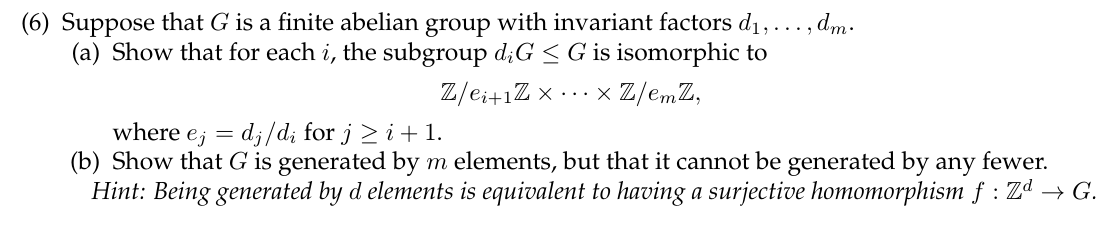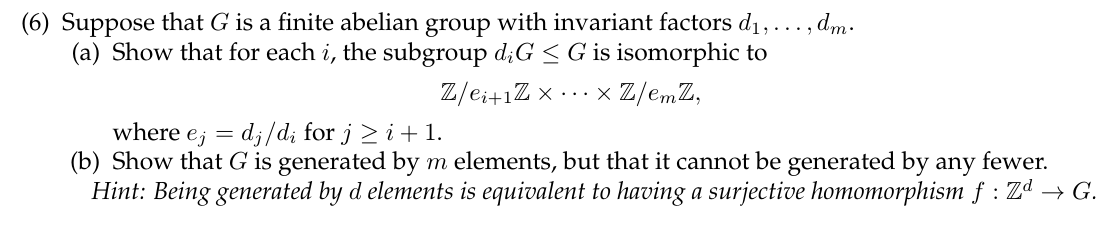
In this homework, all the groups involved will be abelian, and all group operations will be denoted ad- ditively. You are also allowed to use the 'Fundamental theorem of finitely generated abelian groups' which states: Every finitely generated abelian group G is isomorphic to a product Z/dZ x ... Z/dmZ Z", where r is uniquely determined, and the integers d1, ... , dm are uniquely determined by the property di > 2, and di | d2 | ... | dm. The di are called the invariant factors of G. The integer r is called the rank. You will also need the following definition, which will be introduced in class next week: Definition 1. An r x s-matrix A with entries in Z is said to be in Smith normal form if it has the following properties: All the non-zero entries are along the diagonal. If a diagonal entry is zero, then so are all the other diagonal entries after it. If d1, d2, ..., dm are the non-zero diagonal entries in order, then they satisfy d|d2| -- \dm, and di > 1 for all i. (6) Suppose that G is a finite abelian group with invariant factors d1, ..., dm. (a) Show that for each i, the subgroup dig i +1. (b) Show that G is generated by m elements, but that it cannot be generated by any fewer. Hint: Being generated by d elements is equivalent to having a surjective homomorphism f : Zd G. In this homework, all the groups involved will be abelian, and all group operations will be denoted ad- ditively. You are also allowed to use the 'Fundamental theorem of finitely generated abelian groups' which states: Every finitely generated abelian group G is isomorphic to a product Z/dZ x ... Z/dmZ Z", where r is uniquely determined, and the integers d1, ... , dm are uniquely determined by the property di > 2, and di | d2 | ... | dm. The di are called the invariant factors of G. The integer r is called the rank. You will also need the following definition, which will be introduced in class next week: Definition 1. An r x s-matrix A with entries in Z is said to be in Smith normal form if it has the following properties: All the non-zero entries are along the diagonal. If a diagonal entry is zero, then so are all the other diagonal entries after it. If d1, d2, ..., dm are the non-zero diagonal entries in order, then they satisfy d|d2| -- \dm, and di > 1 for all i. (6) Suppose that G is a finite abelian group with invariant factors d1, ..., dm. (a) Show that for each i, the subgroup dig i +1. (b) Show that G is generated by m elements, but that it cannot be generated by any fewer. Hint: Being generated by d elements is equivalent to having a surjective homomorphism f : Zd G