In this problem, we will use a more standard form of the CES utility function to derive indirect utility and expenditure functions. Suppose utility is given by

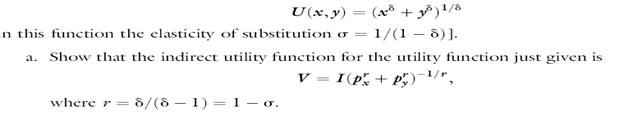
b. Show that the function derived in part (a) is homogeneous of degree 0 in prices and income.

c. Show that this function is strictly increasing in income.

d. Show that this function is strictly decreasing in any price.

e. Show that the expenditure function for this case of CES utility is given by

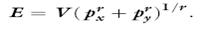
f. Show that the function derived in part (e) is homogeneous of degree 1 in the goods’ prices.

g. Show that this expenditure function is
 
 

(a + )!/8 1/(1 8)]. U(x, y) n this function the clasticity of substitution o = a. Show that the indirect utility function for the utility function just given is V = I(p + P,)", %3D where r = d/(8 1) = 1 -