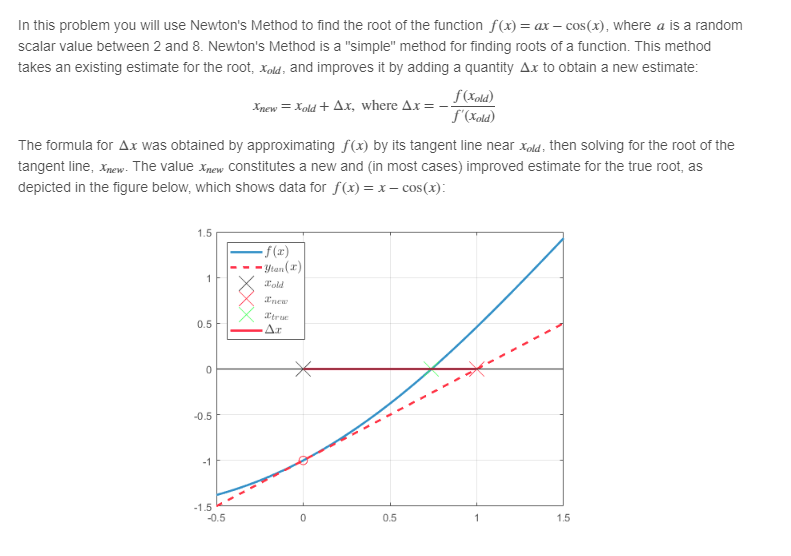
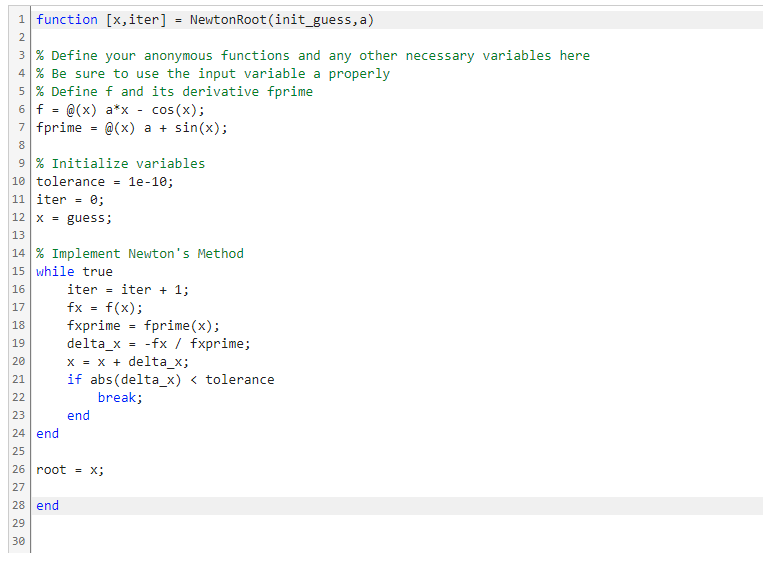
In this problem you will use Newton's Method to find the root of the function f(x) = ax - cos(x), where a is a random scalar value between 2 and 8. Newton's Method is a "simple" method for finding roots of a function. This method takes an existing estimate for the root, xold, and improves it by adding a quantity Ax to obtain a new estimate: Xnew = Xold + Ax, where Ax= The formula for Ax was obtained by approximating f(x) by its tangent line near xold, then solving for the root of the tangent line, Xnew. The value Xnew constitutes a new and (in most cases) improved estimate for the true root, as depicted in the figure below, which shows data for f(x) = x - cos(x): 1.5 0.5 0 -0.5 -1 -1.5 -0.5 -f(x) Ytan (2) Fold Inew Itrue Ar 0 f(xold) f'(Xold) 0.5 1 1.5 This process can be repeated, each time recomputing Ax and replacing the old estimate with the new estimate. Your task is to write a function called NewtonRoot that finds the root of the specified function. Your function should take in an initial guess for the root of the function and then output the value of the root and the numer of iterations required for the alrogithm to converge. An outline of an algorithm using Newton's Method to compute the root of f(x) = ax - cos(x) is provided in the solution template below. : 1. Define f and its derivative fprime corresponding to f(x) = ax cos(x). Do this using anonymous functions so that you can easily evaluate f and fprime for any desired value of x. 2. Set the initial guess for the root (x) equal to the user input to the function. This is the first value of xold- 3. Use the formula above to compute Ax and Xnew- 4. Repeat step 3 until |Ax| < 10-8. This is a reasonable condition for terminating the loop because it means there isn't much change between successive guesses of the root. Note that on successive loops, Xnew from the previous loop should become old for the current loop. You can do this by defining a single variable x and setting up your algorithm properly. Your function should have two inputs: . The first input is the initial guess of the root. . The second input is the variable a, for defining f(x) = ax - cos (x) and f'(x) within the function. Your function should have two outputs: The first output is the value of the root. The second output is the number of iterations required to find the root. For example, if your loop only runs once, the numer of iterations is 1. Notes: Use a while loop in your function. Do not use an existing MATLAB solver to compute the root! In this implementation we only use a single variable, x, to keep track of the current root estimate instead of storing both the new and old values. This is because the old value is no longer needed once the new estimate 1 function [x,iter] NewtonRoot (init_guess, a) 2 3 % Define your anonymous functions and any other necessary variables here 4 % Be sure to use the input variable a properly 5 % Define f and its derivative fprime 6 f = @(x) a*x - cos(x); 7 fprime = @(x) a + sin(x); 8 9 % Initialize variables 10 tolerance = 1e-10; 11 iter = 0; 12 x = guess; 13 14 % Implement Newton's Method 15 while true 16 17 18 19 20 iter iter + 1; fx = f(x); fxprime delta_x = 21 22 23 24 end 25 26 root = x; 27 28 end 29 30 end = = x = x + delta_x; if abs (delta_x) < tolerance break; fprime (x); -fx/ fxprime;