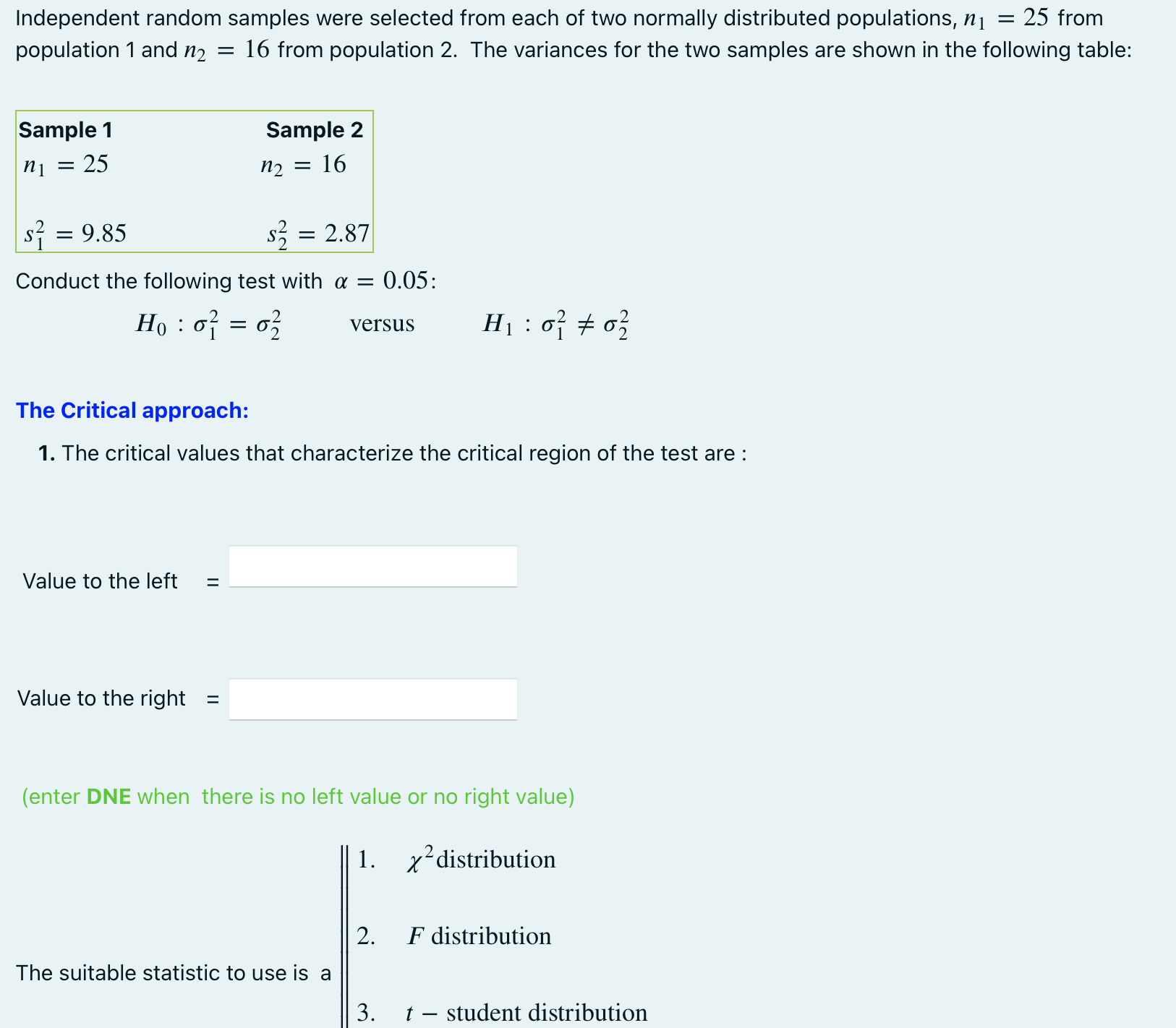
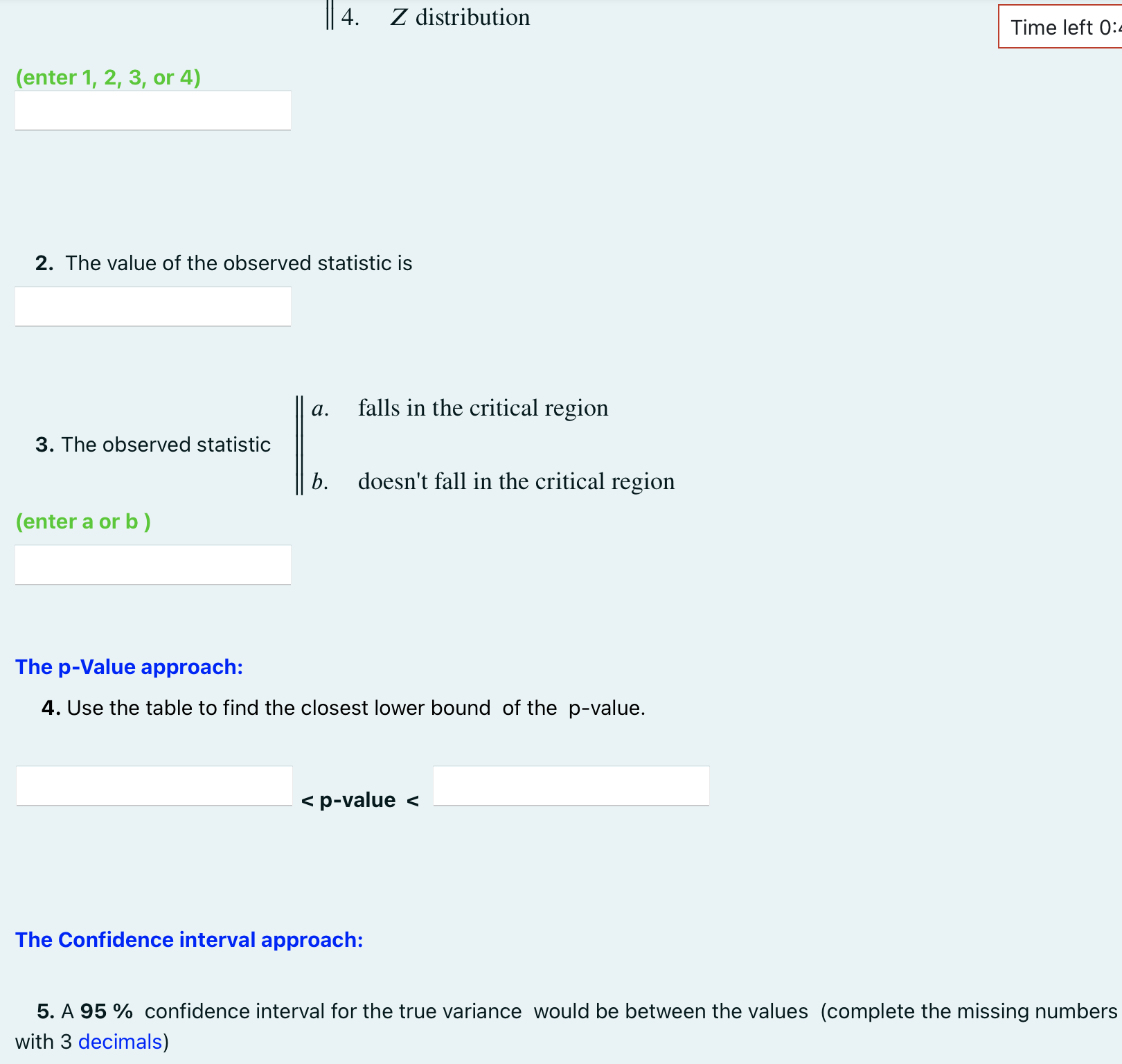
Independent random samples were selected from each of two normally distributed populations, n = : 25 from population 1 and n 16 from population 2. The variances for the two samples are shown in the following table: = Sample 1 n1 25 $ = 9.85 Sample 2 n = 16 s = 2.87 Conduct the following test with = 0.05: H = 0 versus H 0 % 0 The Critical approach: 1. The critical values that characterize the critical region of the test are: Value to the left = Value to the right = (enter DNE when there is no left value or no right value) 1. x distribution 2. F distribution The suitable statistic to use is a 3. t - student distribution (enter 1, 2, 3, or 4) || 4. Z distribution Time left 0:4 2. The value of the observed statistic is a. 3. The observed statistic (enter a or b) falls in the critical region b. doesn't fall in the critical region The p-value approach: 4. Use the table to find the closest lower bound of the p-value. < p-value < The Confidence interval approach: 5. A 95% confidence interval for the true variance would be between the values (complete the missing numbers with 3 decimals) 5. A 95% confidence interval for the true variance would be between the values (complete the missing numbers with 3 decimals) and 6. Select the correct conclusion (enter c or d) c. There is sufficient evidence indicating that it is unlikely that the true variances are equal. d. There is insufficient evidence to indicate that the true variances are different.