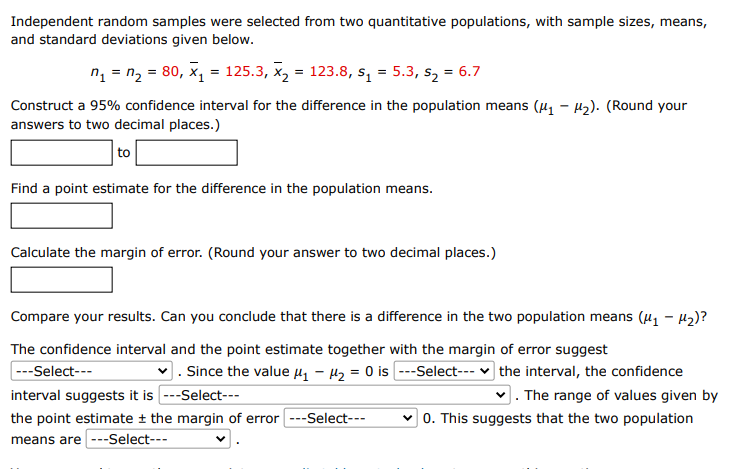
Independent random samples were selected from two quantitative populations, with sample sizes, means, and variances given below. Population 1 2 Sample Size 36 46 Sample Mean 9.5 7.5 Sample Variance 8.32 14.22 Construct a 90% confidence interval for the difference in the population means. (Use - 2. Round your answers to two decimal places.) to Construct a 99% confidence interval for the difference in the population means. (Round your answers to two decimal places.) to What does the phrase "90% confident" or "99% confident" mean? 90% (or 99% as the case may be) of all values from populations 1 and 2 will fall within the interval. Hence, we are fairly certain that this particular interval contains - . There is a 90% (or 99% as the case may be) chance that for any two samples, one sample from population 1 and one sample from population 2, the difference between sample means will fall within the interval. Hence, we are fairly certain that this particular interval contains - . There is a 90% (or 99% as the case may be) probability that the interval will enclose - . Hence, we are fairly certain that this particular interval contains - . In repeated sampling, 90% (or 99% as the case may be) of all intervals constructed in this manner will enclose - . Hence, we are fairly certain that this particular interval contains - - In repeated sampling, 10% (or 1% as the case may be) of all intervals constructed in this manner will enclose - . Hence, we are fairly certain that this particular interval contains - . Independent random samples were selected from two quantitative populations, with sample sizes, means, and variances given below. Population 1 2 Sample Size 49 52 Sample Mean 10.4 8.3 Sample Variance 9.8 15.42 A 90% confidence interval for - is 0.94 to 3.26 and a 99% confidence interval for - is 0.28 to 3.92. Use these confidence intervals to answer the questions. Can you conclude with 99% confidence that there is a difference in the means for the two populations? No. The value - = 0 is not in the interval which does not suggest that there is a difference between and - Yes. The value - = 0 is not in the interval which suggests that there is likely a difference between 1 and 2. Yes. The value - = 0 is in the interval which suggests that there is likely a difference between and - No. The value - = 0 is in the interval which does not suggest that there is a difference between and - Can you conclude with 99% confidence that there is a difference in the means for the two populations? No. The value - = 0 is not in the interval which does not suggest that there is a difference between and . Yes. The value - = 0 is not in the interval which suggests that there is likely a difference between and - - Yes. The value = 0 is in the interval which suggests that there is likely a difference between and - - No. The value = 0 is in the interval which does not suggest that there is a difference between and . Independent random samples were selected from two quantitative populations, with sample sizes, means, and variances given below. Population 1 2 Sample Size 36 36 Sample Mean 5.1 6.6 Sample Variance 9.59 10.22 A 90% confidence interval for - is -2.72 to -0.28 and a 99% confidence interval for - is -3.41 to 0.41. Use these confidence intervals to answer the questions. Can you conclude with 90% confidence that there is a difference in the means for the two populations? No. The value - = 0 is in the interval which does not suggest that there is a difference between and - Yes. The value - = 0 is not in the interval which suggests that there is likely a difference between and . No. The value - = 0 is not in the interval which does not suggest that there is a difference between and Yes. The value - = 0 is in the interval which suggests that there is likely a difference between and . Can you conclude with 99% confidence that there is a difference in the means for the two populations? No. The value - = 0 is in the interval which does not suggest that there is a difference between and - Yes. The value - = 0 is not in the interval which suggests that there is likely a difference between and . No. The value - = 0 is not in the interval which does not suggest that there is a difference between and - Yes. The value - M = 0 is in the interval which suggests that there is likely a difference between and . Independent random samples were selected from two quantitative populations, with sample sizes, means, and standard deviations given below. n = n = 80, x = 125.3, x2 = 123.8, s = 5.3, s = 6.7 - Construct a 95% confidence interval for the difference in the population means (). (Round your answers to two decimal places.) to Find a point estimate for the difference in the population means. Calculate the margin of error. (Round your answer to two decimal places.) Compare your results. Can you conclude that there is a difference in the two population means ( - H)? The confidence interval and the point estimate together with the margin of error suggest ---Select--- interval suggests it is ---Select--- . Since the value - = 0 is ---Select--- the interval, the confidence The range of values given by 0. This suggests that the two population the point estimate the margin of error ---Select--- means are ---Select---