Question
Information for the next two questions: In a used car market, there are 10 identical buyers, each wanting to buy one car. There are 10
Information for the next two questions: In a used car market, there are 10 identical buyers, each wanting to buy one car. There are 10 non-identical sellers indexed by i{1,...,10}. The car of seller i is worth (i1,000)500 to the seller, and (i1,000)+500 to the buyers. For example: car 6 is worth 5,500 to the seller and 6,500 to the buyers. So, i1,000 would be a "fair value'' for car i, such that both buyer and seller would be happy with the transaction.
The problem is that, while the buyers know that there are 10 cars in this market with those valuations, they can't tell one from the other before making the purchase. The sellers know the value of their own car. Buyers and sellers are risk neutral.
An auctioneer (a person who runs an auction) decides the implement the following mechanism to try to solve the informational friction problem:
(1) Set p=10,000 as the "current price'' in the auction.
(2) The auctioneer secretly asks each seller if they would be willing to sell at the current price, and secretly asks each buyer if they would want to buy at that price. (3) If there are buyers and sellers willing to transact, the auctioneer matches the willing buyers and willing sellers at random. Then, the matched buyer pays the current price and gets the car from the matched seller. The matched buyers and sellers leave the auction. (4) Next, the auctioneer decreases the "current price'' by 1,000 and goes back to step (2). The auction ends when the price reaches zero.
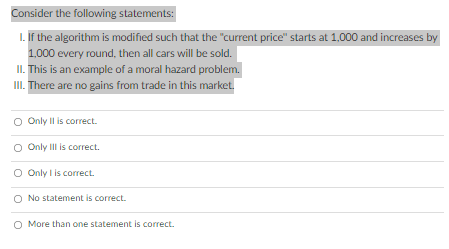
Question 21: What is the equilibrium outcome of this algorithm? Hint: which sellers are willing to sell at the "current price'', and what will the buyer infer from that?

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


