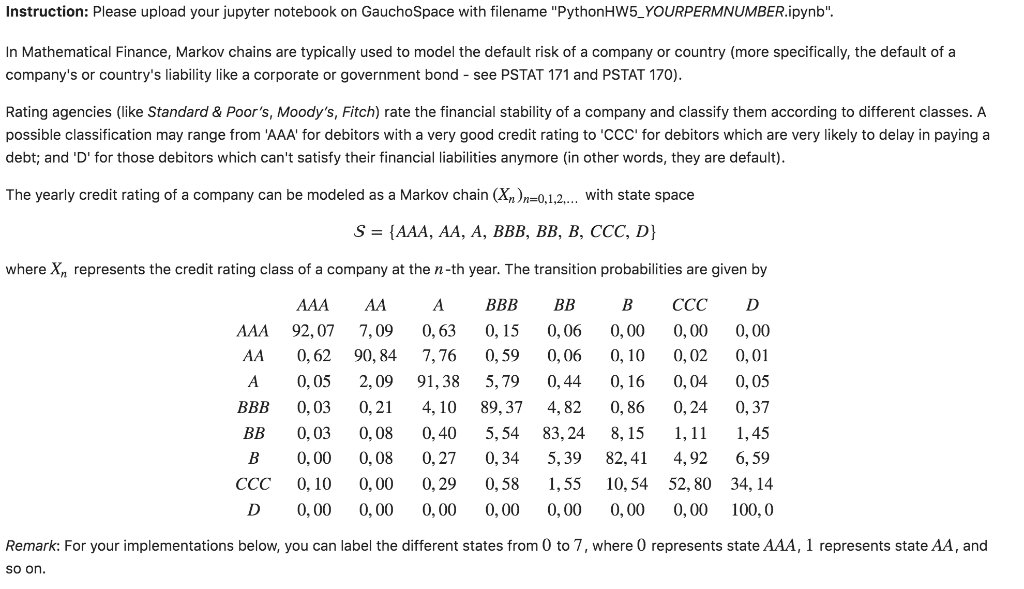
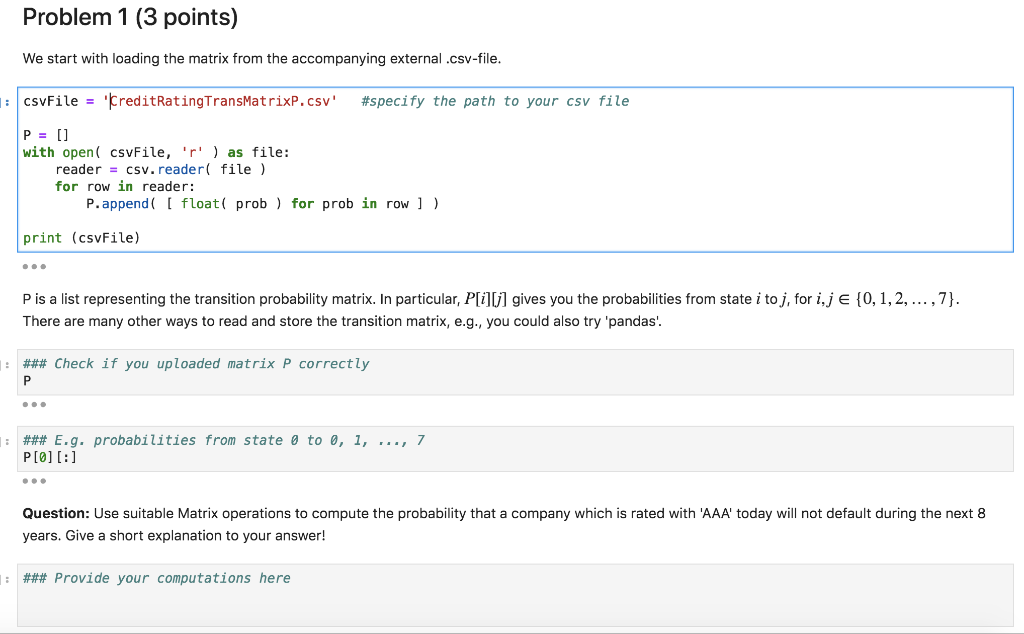
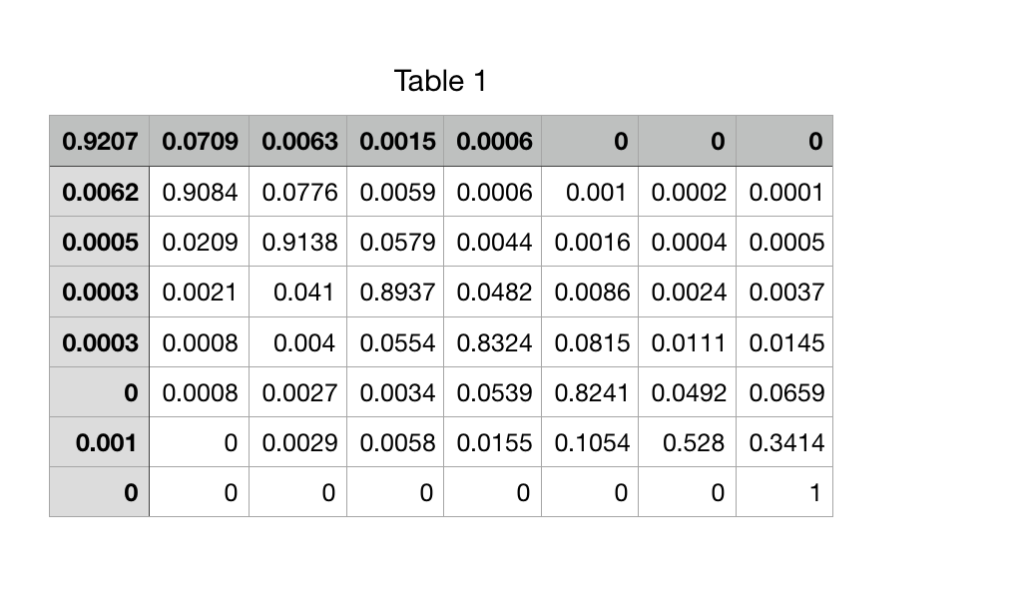
Instruction: Please upload your jupyter notebook on GauchoSpace with filename "PythonHW5_YOURPERMNUMBER.ipynb". In Mathematical Finance, Markov chains are typically used to model the default risk of a company or country (more specifically, the default of a company's or country's liability like a corporate or government bond - see PSTAT 171 and PSTAT 170). Rating agencies (like Standard & Poor's, Moody's, Fitch) rate the financial stability of a company and classify them according to different classes. A possible classification may range from 'AAA' for debitors with a very good credit rating to 'CCC' for debitors which are very likely to delay in paying a debt; and 'D' for those debitors which can't satisfy their financial liabilities anymore (in other words, they are default). The yearly credit rating of a company can be modeled as a Markov chain (-0,1..with state space where Xn represents the credit rating class of a company at the n-th year. The transition probabilities are given by AAA AA A BBB BB BcCC D AAA 92,07 7,09 0,63 0,15 0,06 0,00 0,00 0,00 AA 0,62 90,84 7,76 0,59 0,06 0,10 0,02 0,01 A 0,05 2,09 91,38 5,79 0,44 0,16 0,04 0,05 BBB 0,03 0,2 4,10 89,37 4,82 0, 86 0,24 0,37 BB 0, 03 0,08 0,40 5,54 83,24 8,151,11 1,45 0,00 0,08 0,27 0,34 5,39 82,41 4,92 6,59 ccc 0, 10 0,00 0,29 0,58 ,55 10,54 52,80 34,14 D 0,00 0,00 0,00 0,00 0,00 0,00 0,00 100,0 Remark: For your implementations below, you can label the different states from 0 to 7, where 0 represents state AAA, represents state A, and so on. Problem 1 (3 points) We start with loading the matrix from the accompanying external .csv-file csvFle-treditRatingTransMatrixp.csv' #specify the path to your csv file with open( csvFile, 'r' as file: reader csv. reader file) for row in reader: P.append float prob) for prob in row ] print (csvFile) 0.0 P is a list representing the transition probability matrix. In particular, P[iU] gives you the probabilities from state i toj, for i,j {0, , 2, There are many other ways to read and store the transition matrix, e.g., you could also try 'pandas , 7). ### Check if you uploaded matrix P correctly : ### E.g. probabilities from state 0 to 0, 1, , 7 0.0 Question: Use suitable Matrix operations to compute the probability that a company which is rated with 'AAA' today will not default during the next 8 years. Give a short explanation to your answer! ### Provide your computations here Table 1 0.9207 0.0709 0.0063 0.0015 0.0006 0 0 0 0.0062 0.9084 0.0776 0.0059 0.0006 0.001 0.0002 0.0001 0.0005 0.0209 0.9138 0.0579 0.0044 0.0016 0.0004 0.0005 0.0003 0.00210.040.89370.0482 0.0086 0.0024 0.0037 0.0003 0.0008 0.004 0.0554 0.8324 0.0815 0.0111 0.0145 0 0.0008 0.0027 0.0034 0.0539 0.8241 0.0492 0.0659 0 0.0029 0.0058 0.0155 0.10540.528 0.3414 0.001 0 0 0 0 Instruction: Please upload your jupyter notebook on GauchoSpace with filename "PythonHW5_YOURPERMNUMBER.ipynb". In Mathematical Finance, Markov chains are typically used to model the default risk of a company or country (more specifically, the default of a company's or country's liability like a corporate or government bond - see PSTAT 171 and PSTAT 170). Rating agencies (like Standard & Poor's, Moody's, Fitch) rate the financial stability of a company and classify them according to different classes. A possible classification may range from 'AAA' for debitors with a very good credit rating to 'CCC' for debitors which are very likely to delay in paying a debt; and 'D' for those debitors which can't satisfy their financial liabilities anymore (in other words, they are default). The yearly credit rating of a company can be modeled as a Markov chain (-0,1..with state space where Xn represents the credit rating class of a company at the n-th year. The transition probabilities are given by AAA AA A BBB BB BcCC D AAA 92,07 7,09 0,63 0,15 0,06 0,00 0,00 0,00 AA 0,62 90,84 7,76 0,59 0,06 0,10 0,02 0,01 A 0,05 2,09 91,38 5,79 0,44 0,16 0,04 0,05 BBB 0,03 0,2 4,10 89,37 4,82 0, 86 0,24 0,37 BB 0, 03 0,08 0,40 5,54 83,24 8,151,11 1,45 0,00 0,08 0,27 0,34 5,39 82,41 4,92 6,59 ccc 0, 10 0,00 0,29 0,58 ,55 10,54 52,80 34,14 D 0,00 0,00 0,00 0,00 0,00 0,00 0,00 100,0 Remark: For your implementations below, you can label the different states from 0 to 7, where 0 represents state AAA, represents state A, and so on. Problem 1 (3 points) We start with loading the matrix from the accompanying external .csv-file csvFle-treditRatingTransMatrixp.csv' #specify the path to your csv file with open( csvFile, 'r' as file: reader csv. reader file) for row in reader: P.append float prob) for prob in row ] print (csvFile) 0.0 P is a list representing the transition probability matrix. In particular, P[iU] gives you the probabilities from state i toj, for i,j {0, , 2, There are many other ways to read and store the transition matrix, e.g., you could also try 'pandas , 7). ### Check if you uploaded matrix P correctly : ### E.g. probabilities from state 0 to 0, 1, , 7 0.0 Question: Use suitable Matrix operations to compute the probability that a company which is rated with 'AAA' today will not default during the next 8 years. Give a short explanation to your answer! ### Provide your computations here Table 1 0.9207 0.0709 0.0063 0.0015 0.0006 0 0 0 0.0062 0.9084 0.0776 0.0059 0.0006 0.001 0.0002 0.0001 0.0005 0.0209 0.9138 0.0579 0.0044 0.0016 0.0004 0.0005 0.0003 0.00210.040.89370.0482 0.0086 0.0024 0.0037 0.0003 0.0008 0.004 0.0554 0.8324 0.0815 0.0111 0.0145 0 0.0008 0.0027 0.0034 0.0539 0.8241 0.0492 0.0659 0 0.0029 0.0058 0.0155 0.10540.528 0.3414 0.001 0 0 0 0