Intro The risk-free asset pays a return of rF=0.5%. There are 3 risky assets: A, B and C. The expected returns and variances of

Question

23 users unlocked this solution today!

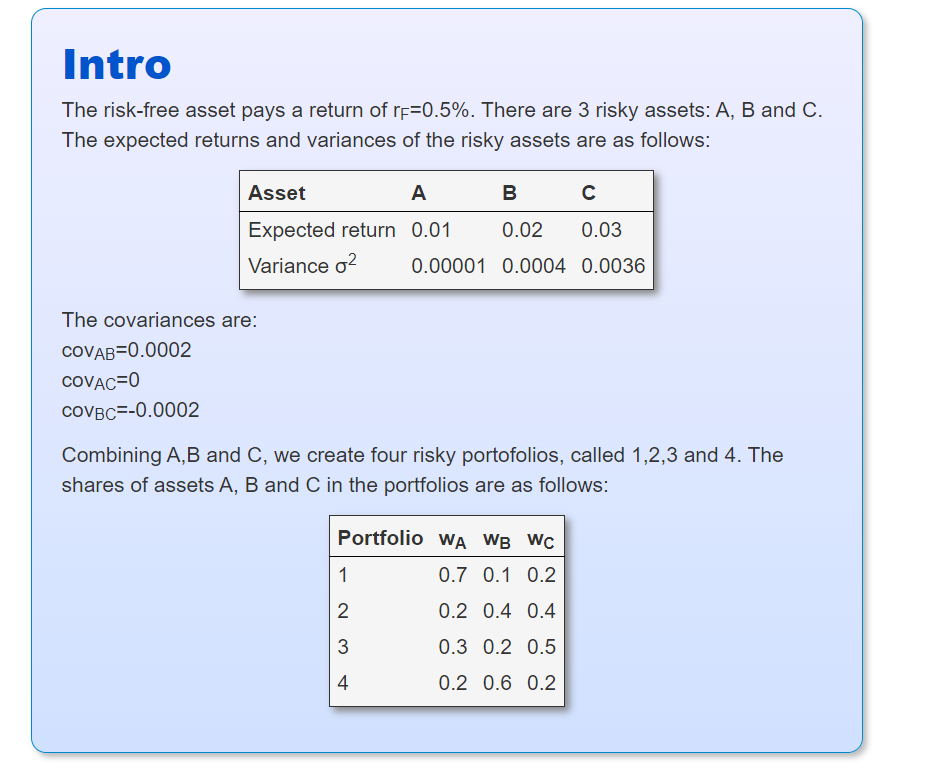
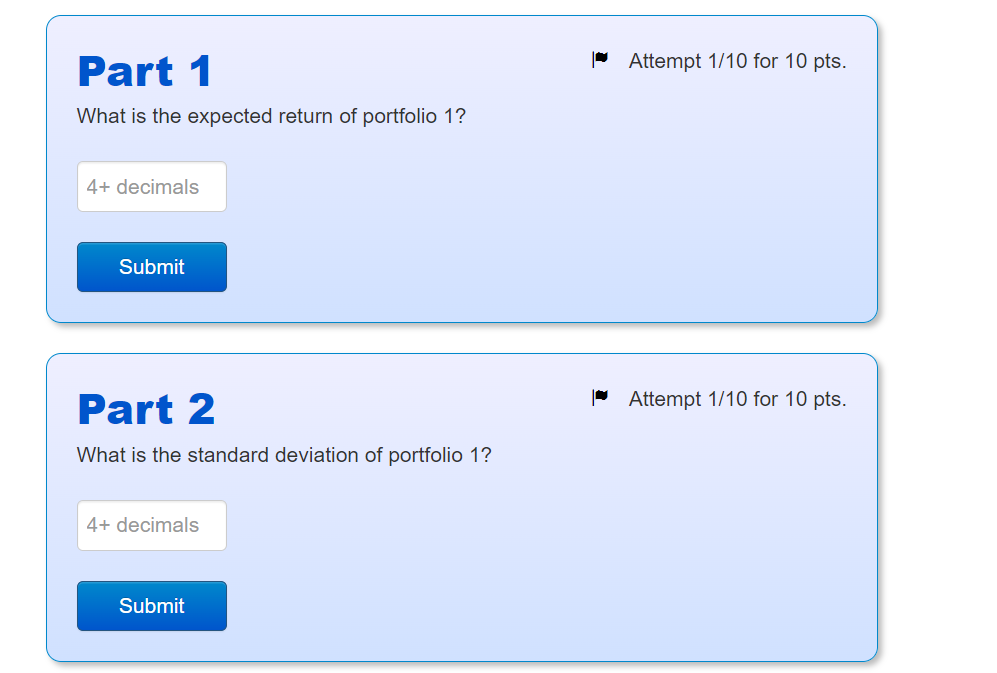
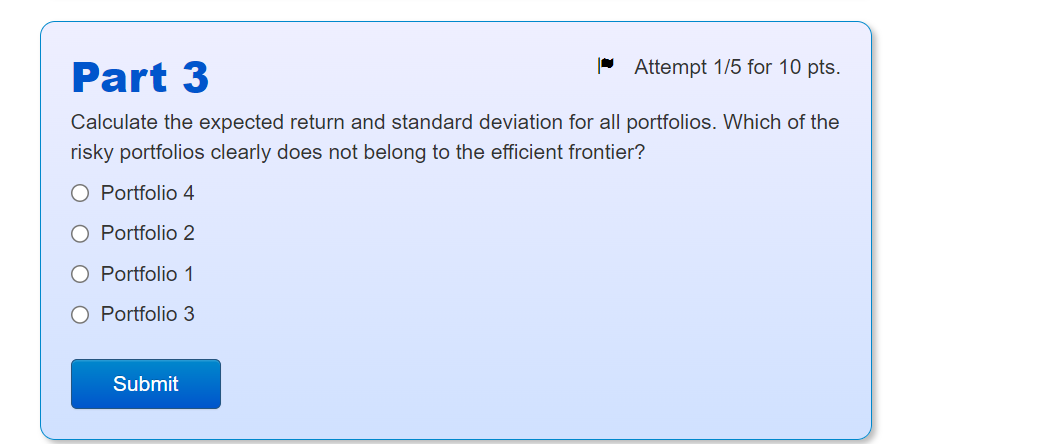
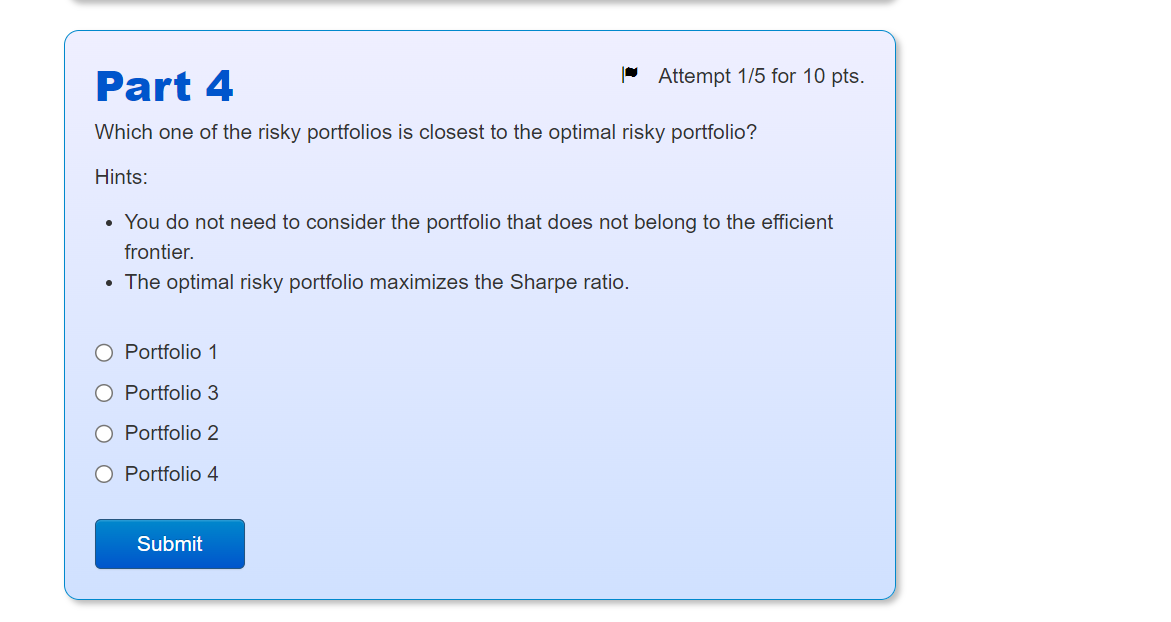
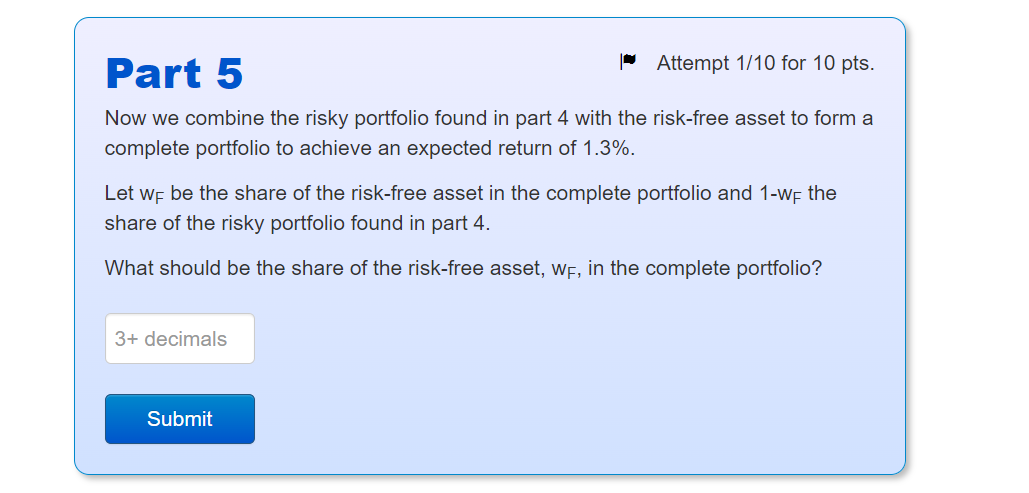
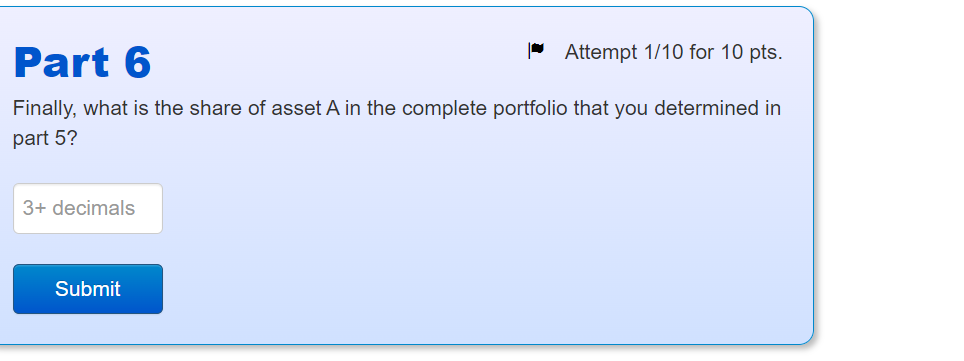
Intro The risk-free asset pays a return of rF=0.5%. There are 3 risky assets: A, B and C. The expected returns and variances of the risky assets are as follows: Asset A Expected return 0.01 Variance o The covariances are: COVAB=0.0002 COVAC=0 COVBC=-0.0002 B 0.02 0.03 0.00001 0.0004 0.0036 Combining A, B and C, we create four risky portofolios, called 1,2,3 and 4. The shares of assets A, B and C in the portfolios are as follows: Portfolio WA WB WC 0.7 0.1 0.2 1 2 3 4 0.2 0.4 0.4 0.3 0.2 0.5 0.2 0.6 0.2 Part 1 What is the expected return of portfolio 1? 4+ decimals Submit Part 2 What is the standard deviation of portfolio 1? 4+ decimals Submit Attempt 1/10 for 10 pts. Attempt 1/10 for 10 pts. Attempt 1/5 for 10 pts. Part 3 Calculate the expected return and standard deviation for all portfolios. Which of the risky portfolios clearly does not belong to the efficient frontier? Portfolio 4 Portfolio 2 Portfolio 1 O Portfolio 3 Submit Part 4 Which one of the risky portfolios is closest to the optimal risky portfolio? Hints: Attempt 1/5 for 10 pts. You do not need to consider the portfolio that does not belong to the efficient frontier. The optimal risky portfolio maximizes the Sharpe ratio. Portfolio 1 Portfolio 3 Portfolio 2 O Portfolio 4 Submit Part 5 Now we combine the risky portfolio found in part 4 with the risk-free asset to form a complete portfolio to achieve an expected return of 1.3%. Attempt 1/10 for 10 pts. Let WF be the share of the risk-free asset in the complete portfolio and 1-w- the share of the risky portfolio found in part 4. What should be the share of the risk-free asset, WF, in the complete portfolio? 3+ decimals Submit Part 6 Finally, what is the share of asset A in the complete portfolio that you determined in part 5? 3+ decimals Attempt 1/10 for 10 pts. Submit Problem 4 Intro You have $7,000 to invest. You've done some security analysis and generated the following data for three stocks and Treasury bills, including weights in the optimal risky portfolio (ORP) from doing Markowitz portfolio optimization: Security Expected return (%) Variance Beta Weight in ORP (%) Stock A Stock B Stock C 12 7 5 0.04 0.03 0.02 1.2 1.5 0.8 48 18 34 T-bills 4 0 0 0 Part 1 If you want to achieve an expected return of 7% for the complete portfolio, how much money should you invest in stock B (in $)? 0+ decimals Submit Attempt 3/10 for 10 pts. 0+ decimals Part 2 What is the ratio of the Sharpe ratio of the complete portfolio to the Sharpe ratio of the ORP? Submit Attempt 2/10 for 10 pts.