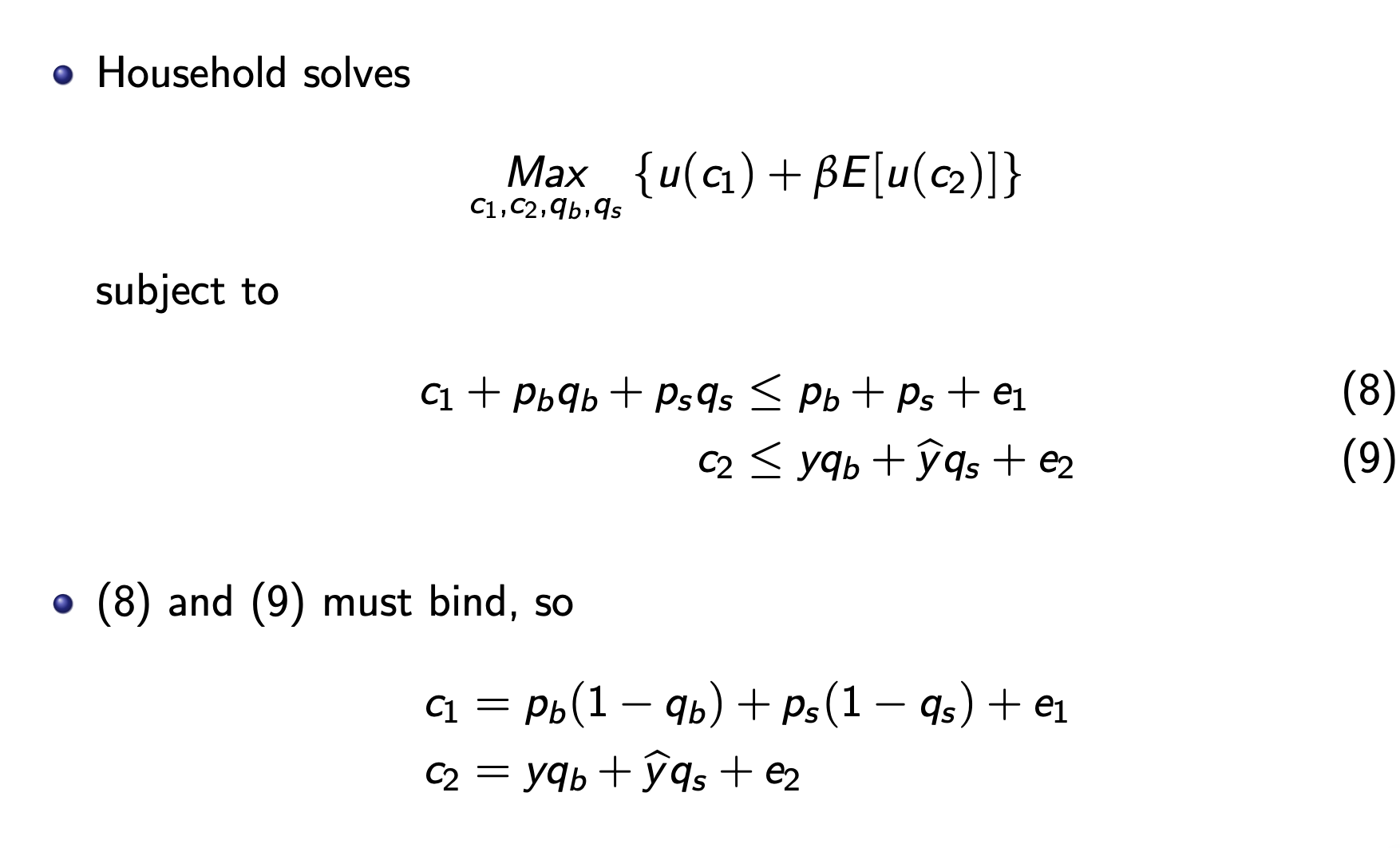
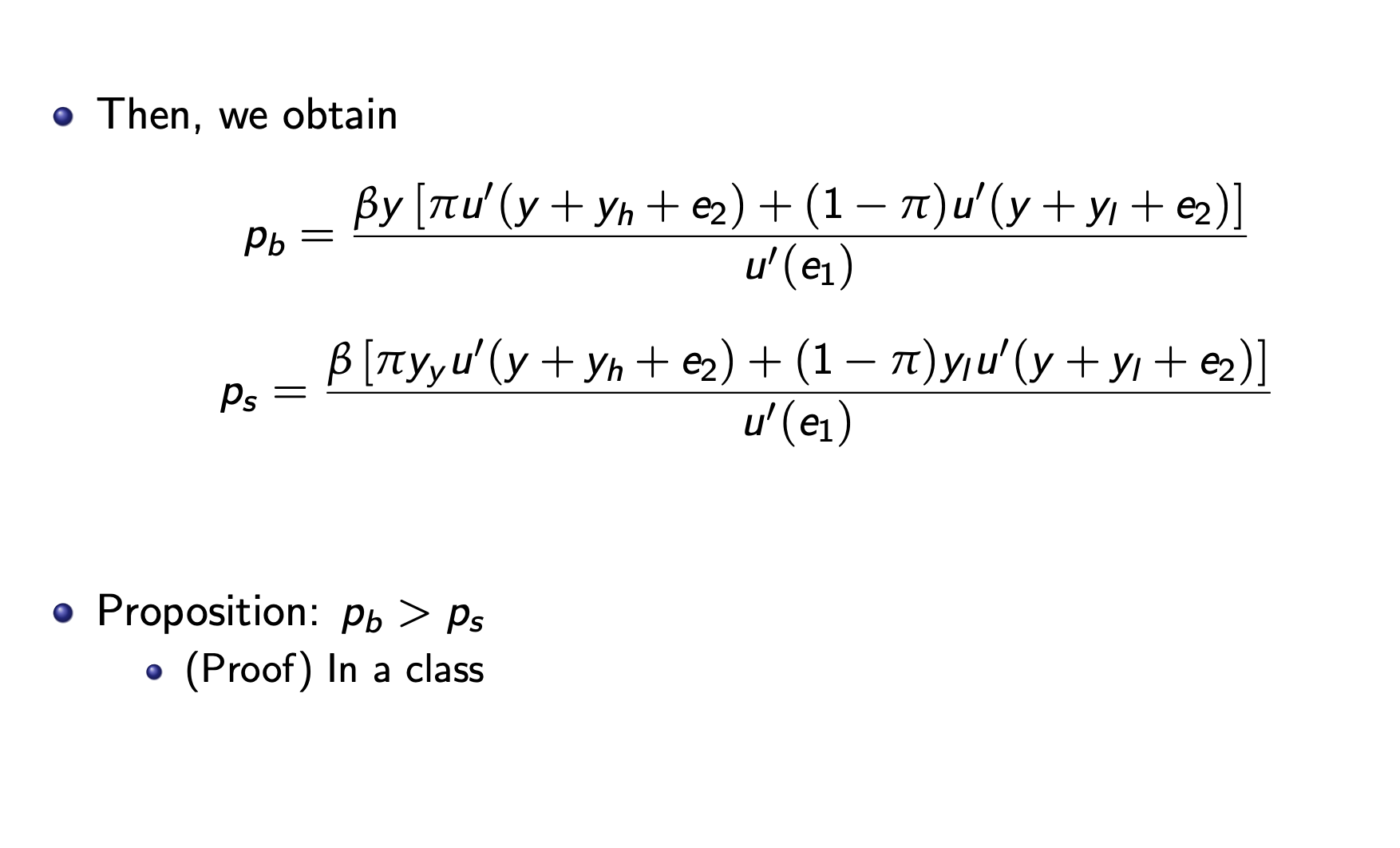
Introduce uncertainty into the model At t = 2, each stock gives stochastic dividend as = { = {y/h with probability with probability 1 )y - Let y = E[y] = h + (1 ) At t = 2, each bond gives y units of consumption goods with certainty Thus, expected dividend of stocks is same with that of bonds Consumption c at t = 2 depends on realization of dividend state of stock Thus, we introduce the concept of expected utility: E[u(c2)] Household solves subject to Max {u(c) + BE[u(c2)]} C1, C2,96,9s C1 + Pbqb + Psqs Pb + Ps + e1 (8) C yqb +qs + ez (9) (8) and (9) must bind, so C1 = Pb(19b) Ps (1 - 9s) + e1 C2 C = qb + qs + ez Using binding, (8) and (9), write the problem as Max 9b,9s { - - u(Pb(1 q) + Ps (1 9s) + e1) +[u(qb+hs + 2) + (1 )u(qb + qs+ e2)] - FOCs are u' (C1) Pb = | yu' (c) + (1 )yu' (c) - u' (C1)ps = [ ynu' (c) + (1 )yu' (C)] where c = yqb + y;qs + e2 for i = h,l Market clearing conditions are qb C1 = e1 ch = y + yh + e c = y + y + 2 == 9s = 1, so Then, we obtain Pb = Ps = [u' (y + h + 2) + (1 )u' (y + y + e2)] u' (e1) [yu' (y +h + e) + (1 ) u' (y + y + e)] u' (e1) - Proposition: Pb > Ps (Proof) In a class 3) Consider the asset pricing model with uncertainty in the slide. We derived the asset prices as Pb = Ps = - [nu' (y+Yn + e) + (1 )u' (y + y + e)] u'(e1) [nu' (y +n + ) + (1 )u' (y + y + e2)] u'(e1) in the class. We showed that p > Ps in the class if u" (x) < 0 for all x > 0. Now prove that p = Ps if u"(x) = 0 for all x > 0. (Hint: u" (x) = 0 for all x>0 means that u'(x) is constant for all x > 0)