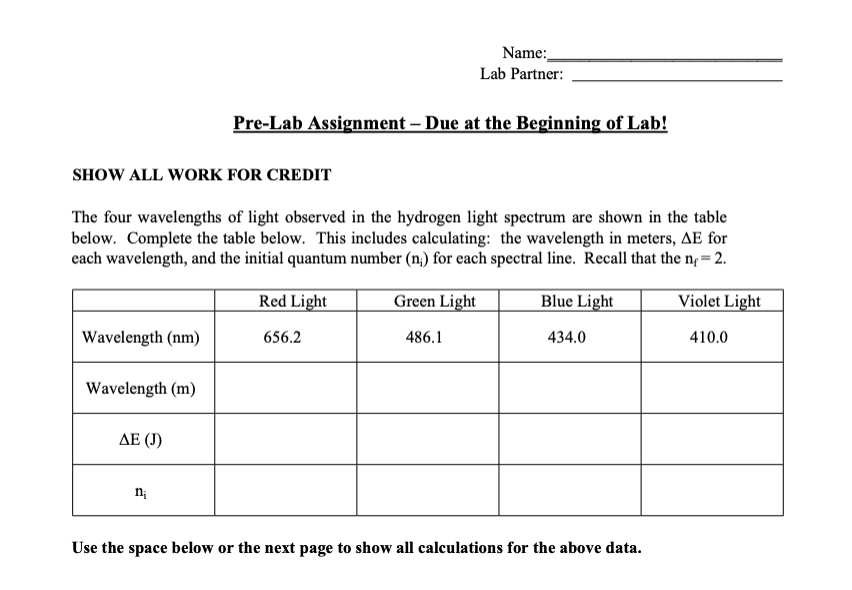
Introduction Celebration of holidays with fireworks illuminates the night sky with brilliant colors created by metal ions. The metals used to create fireworks are chosen to create specific colors. The colors are created by excitation and subsequent relaxation of electrons in metals. Electrons occupy discrete energy levels, which increase in energy as you move away from the nucleus, and electrons cannot exist between these levels. To transition from one level to another, a specific amount of energy must be emitted or absorbed. When electrons relax (or move down an energy level) energy is emitted. To move up an energy level, an electron must absorb energy. For an electron, the change in energy (E) can be calculated as follows: E=hc where is the wavelength of light in meters, h is Planck's constant (6.6261034Js) and c is the speed of light (2.998108m/s) The energy emitted or absorbed can be used to identify the quantum number of the energy level the electron occupied, which is denoted as n. The quantum number n is always an integer greater than or equal to 1 . When all electrons occupy the lowest energy levels possible, the atom is considered to be in the around state. For example, hydrogen is in the ground state when its single electron is in the orbital where n=1. If an electron is in an orbital that is higher than the lowest energy levels possible, the atom is in an excited state. For hydrogen, an electron in any orbital above n=1 is excited. There can be more than one excited state and electrons can relax between individual excited states. For visible light emitted by hydrogen, an electron's quantum number (n) can be calculated using Bohr's equation as follows: E=(2.181018J)(nf21ni21) where E is the change in energy, nf is the quantum number of the final orbital, and ni is the quantum number of the initial orbital. For hydrogen, the visible spectral lines all have an nf=2, which makes the initial quantum number easy to calculate. For multi-electron elements, the calculations become complicated and Bohr's equation is insufficient. Excited electrons still emit photons and the magnitude of the energy change is dependent upon the energy levels being transitioned between. The number and type of transition depend upon the energy level structure of the chemical species and quantum selection rules. While we will not complete these types of calculations, you should recognize that each element has characteristic emission energies, which may consist of a large number of discrete wavelengths. We can use these unique wavelength profiles to our advantage. In addition to creating fireworks, we can create specific color of light in light bulbs. However, the majority of light we observe is from continuous emission spectra. This light appears white, but is actually a rainbow of colors. These are commonly seen when the source of light is a solid. The atoms and molecules in heated solids continuously bump into each other due to close packing. This transforms the excitation energy into kinetic energy, which is not quantized. A spectroscope is an instrument that measures the wavelengths of light emitted from a light source. Figure 1 shows a diagram of the spectroscope we will use for this lab. The slit (upper right) allows light to enter the spectroscope. The light travels to a diffraction grating, which reflects and refracts the light back towards a scale at the far end of the spectroscope. This grating bends the light like a prism allowing the colors to split across the scale in discrete wavelengths. The numbers on the scale are roughly equivalent to the associated wavelength. For example, a 5 on the scale is equivalent to 500nm. To use the spectroscope, we look through the viewing port and align the slit with the light source. Once properly aligned, the spectrum will appear on the scale. The end result can be very fait and difficult to observe! We will calibrate the spectroscope using a fluorescent light. Fluorescent lights use a combination of elements to produce visible light. The most common elements are listed in Table 1. We will then use the calibrated spectroscope to determine the prominent spectral lines and approximate wavelengths for four metal ions and an unknown metal ion mixture that you will identify. Table 1 - Common Elements in Fluorescent Light Bulbs Student Learning Objectives: This activity will allow the student to observe the wavelength of light emitted by various elements and light sources. Upon completion of this laboratory, the student will be able to: a. describe the relationship between energy and wavelength of light. b. utilize a spectroscope to evaluate emission spectra of various light sources c. identify the spectrum lines for 4 known metals and use them to identify an unknown metal. d. calculate hydrogen quantum numbers. SHOW ALL WORK FOR CREDIT The four wavelengths of light observed in the hydrogen light spectrum are shown in the table below. Complete the table below. This includes calculating: the wavelength in meters, E for each wavelength, and the initial quantum number (ni) for each spectral line. Recall that the nf=2. Use the space below or the next page to show all calculations for the above data