Introduction

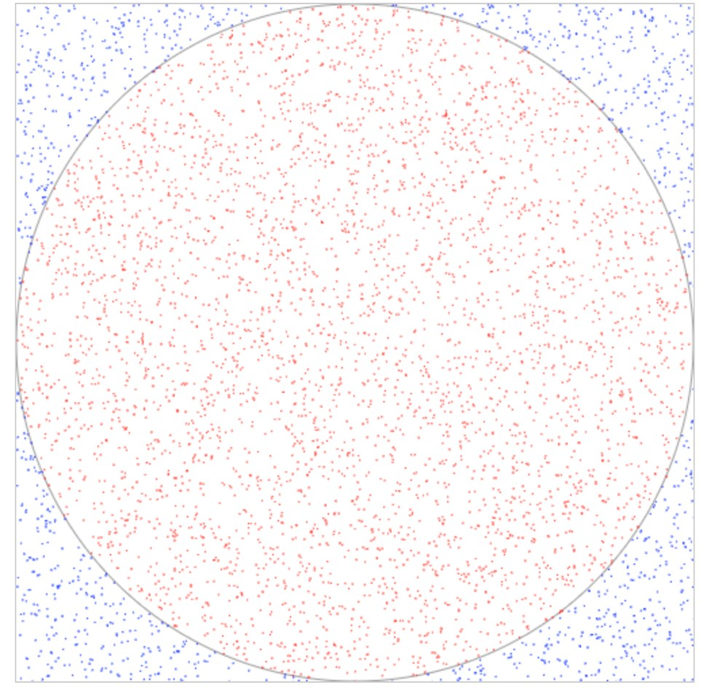
How to estimate a value of using the Monte Carlo method - generate a large number of random points and see how many fall in the circle enclosed by the unit square. One method to estimate the value of (3.141592...) is by using a Monte Carlo method. We can have a circle of radius 0.5, enclosed by a 1 1 square. The area of the circle is r² = /4, the area of the square is 1. If we divide the area of the circle, by the area of the square we get /4.

We then generate a large number of uniformly distributed random points and plot them on the graph. These points can be in any position within the square i.e. between (0,0) and (1,1). If they fall within the circle, they are coloured red, otherwise they are coloured blue. We keep track of the total number of points, and the number of points that are inside the circle. If we divide the number of points within the circle, N_inner by the total number of points, N_total, we should get a value that is an approximation of the ratio of the areas we calculated above, /4. In other words: /4 = N_inner/N_total, and = 4 N_inner/N_total.

When we only have a small number of points, the estimation is not very accurate, but when we have hundreds of thousands of points, we get much closer to the actual value - to within around 2 decimal places of accuracy.

Write a Python program to simulate the calculation of using Monte Carlo method. Your program draws the circle and the square, and plot the random points in the graph as shown in Figure 1. You need simulate different numbers of points (at least include 10, 500, 1,000, 5,000, 10,000, 50,000, 80,000, 100,000, 200,000) and calculate the value for each different number of points. Then draw a line chart to show the change of the accuracy of the value of calculated when the number of points is increased.

Submit Python code (2 points, no point will be given for a program that doesnt correctly implement the simulation algorithm), and simulation results including the graph plots (1 point), values (1 point), and line chart (1 point).