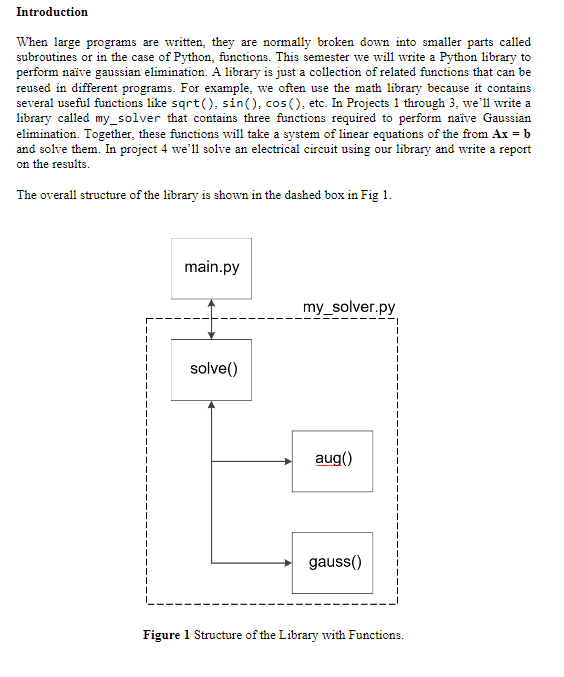
Introduction When large programs are written, they are normally broken down into smaller parts called subroutines or in the case of Python, functions. This semester we will write a Python library to perform nave gaussian elimination. A library is just a collection of related functions that can be reused in different programs. For example, we often use the math library because it contains several useful functions like sqrt(), sin(), cos (), etc. In Projects 1 through 3, we'll write a library called my_solver that contains three functions required to perform nave Gaussian elimination. Together, these functions will take a system of linear equations of the from Ax = b and solve them. In project 4 we'll solve an electrical circuit using our library and write a report on the results. The overall structure of the library is shown in the dashed box in Fig 1. main.py solve() my_solver.py aug() gauss() Figure 1 Structure of the Library with Functions. The program called main, is not part of the library but uses the library just like we use the math library. Main will set up the problem by forming the A and b matrices for a system of linear equations and pass them to the function solve. Then solve will call aug to form the augmented matrix [A]b]. The augmented matrix will then be passed to the function gauss which will perform nave Gaussian elimination on [Alb]. The resulting echelon form of the augmented matrix will be returned to solve. Back substitution will be performed and solve will return the solution to the main program. A very high level pseudo code for performing nave Gaussian elimination can be written as: augment matrices A and B perform gaussian elimination # done in aug() # done in gauss() #done in solve() perform back substitution We've broken done a large programming problem into small pieces that we implement in functions. We program those functions in a library so that we can easily import them and use whenever we need them. Also notice that the program performs Gaussian elimination just like we do when solving by hand. The Augmented Matrix Function Project 1 requires a documented function named aug that forms an augmented matrix from two matrices passed to it. The use of for loops is required to perform the augmentation. The function should return the augmented matrix to the calling program. Include error checking to ensure both matrices to be augmented have the same number of rows. If they do not, display a descriptive error message and stop rogram execution. The function should be in a Python file that you name my solver.py, NOT in a file called aug. py. To use aug in a program, we'll need to import the library with import my_solver as ms and then call the function with ms.aug(). Do not assume that either matrix is a vector. This will allow the function to be more general so that it can be used for situations where we might want to augment a given matrix with the identity matrix. Pseudo Code for the Augmented Matrix Function For full credit, your function must follow this pseudo code and you can not use any functions we have not discussed in class. Significant points will be lost if this criteria is not followed. find rows m and columns n in A find rows m2 and columns n2 in B if mm print error message saying rows must be equal stop # Find size of the augmented matrix aux_A rows in aug_A = rows in A (or we could use rows in B) columns in aug_A columns in A+ columns in B initialize empty aug A matrix # Copy A into aug_A for i to m for je to n Copy contents of A, into aug_A,5 # Append B to the right of A in the augmented matrix for i 0 to m for j 0 to n Copy contents of B, into aug_A, 5+1 = Introduction When large programs are written, they are normally broken down into smaller parts called subroutines or in the case of Python, functions. This semester we will write a Python library to perform nave gaussian elimination. A library is just a collection of related functions that can be reused in different programs. For example, we often use the math library because it contains several useful functions like sqrt(), sin(), cos (), etc. In Projects 1 through 3, we'll write a library called my_solver that contains three functions required to perform nave Gaussian elimination. Together, these functions will take a system of linear equations of the from Ax = b and solve them. In project 4 we'll solve an electrical circuit using our library and write a report on the results. The overall structure of the library is shown in the dashed box in Fig 1. main.py solve() my_solver.py aug() gauss() Figure 1 Structure of the Library with Functions. The program called main, is not part of the library but uses the library just like we use the math library. Main will set up the problem by forming the A and b matrices for a system of linear equations and pass them to the function solve. Then solve will call aug to form the augmented matrix [A]b]. The augmented matrix will then be passed to the function gauss which will perform nave Gaussian elimination on [Ab]. The resulting echelon form of the augmented matrix will be returned to solve. Back substitution will be performed and solve will return the solution to the main program. A very high level pseudo code for performing nave Gaussian elimination can be written as: augment matrices A and B perform gaussian elimination # done in aug() # done in gauss() #done in solve() perform back substitution We've broken done a large programming problem into small pieces that we implement in functions. We program those functions in a library so that we can easily import them and use whenever we need them. Also notice that the program performs Gaussian elimination just like we do when solving by hand. The Augmented Matrix Function Project 1 requires a documented function named aug that forms an augmented matrix from two matrices passed to it. The use of for loops is required to perform the augmentation. The function should return the augmented matrix to the calling program. Include error checking to ensure both matrices to be augmented have the same number of rows. If they do not, display a descriptive error message and stop rogram execution. The function should be in a Python file that you name my_solver.py, NOT in a file called aug.py. To use aug in a program, we'll need to import the library with import my_solver as ms and then call the function with ms.aug(). Do not assume that either matrix is a vector. This will allow the function to be more general so that it can be used for situations where we might want to augment a given matrix with the identity matrix. Pseudo Code for the Augmented Matrix Function For full credit, your function must follow this pseudo code and you can not use any functions we have not discussed in class. Significant points will be lost if this criteria is not followed. find rows m and columns n in A find rows m2 and columns n2 in B if mm print error message saying rows must be equal stop # Find size of the augmented matrix aux A rows in aug_A = rows in A (or we could use rows in B) columns in aug_A columns in A+ columns in B initialize empty aug A matrix # Copy A into aug_A for i to m for j to n Copy contents of A, into aug_A,5 # Append B to the right of A in the augmented matrix for i 0 to m for j 0 to n Copy contents of B, into aug_A, 5+1 =