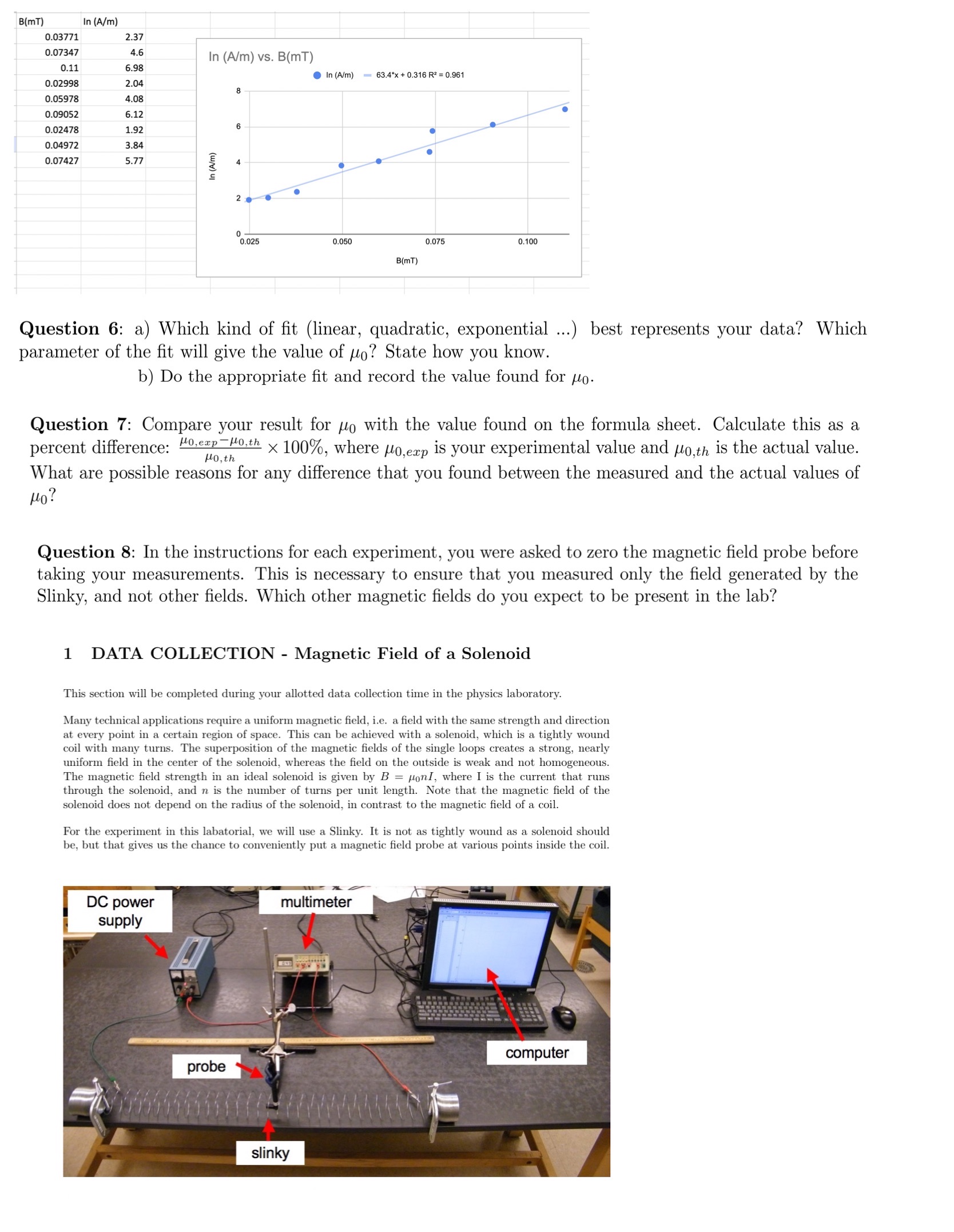
It is a collecting data for lab, and we need to solve some question here. Based on the Lab Manual ( 1 Data Collection) and the graphing here. Please help me to answer question 6-8. Thanks so much in advance.

B(mT) In (A/m) 0.03771 2.37 0.07347 4.6 In (A/m) vs. B(mT) 0.11 6.98 In (A/m) - 63.4*x + 0.316 R2 = 0.961 0.0299 2.04 0.05978 4.08 0.09052 6.12 0.02478 1.92 0.04972 3.84 0.07427 5.77 In (A 0.025 0.050 0.075 0.100 B(mT) Question 6: a) Which kind of fit (linear, quadratic, exponential ...) best represents your data? Which parameter of the fit will give the value of Mo? State how you know. b) Do the appropriate fit and record the value found for Mo. Question 7: Compare your result for Mo with the value found on the formula sheet. Calculate this as a percent difference: Ho , th : Ho,exp-HO.th x 100%, where Mo,exp is your experimental value and Mo,th is the actual value. What are possible reasons for any difference that you found between the measured and the actual values of Ho! Question 8: In the instructions for each experiment, you were asked to zero the magnetic field probe before taking your measurements. This is necessary to ensure that you measured only the field generated by the Slinky, and not other fields. Which other magnetic fields do you expect to be present in the lab? 1 DATA COLLECTION - Magnetic Field of a Solenoid This section will be completed during your allotted data collection time in the physics laboratory. Many technical applications require a uniform magnetic field, i.e. a field with the same strength and direction at every point in a certain region of space. This can be achieved with a solenoid, which is a tightly wound coil with many turns. The superposition of the magnetic fields of the single loops creates a strong, nearly uniform field in the center of the solenoid, whereas the field on the outside is weak and not homogeneous. The magnetic field strength in an ideal solenoid is given by B = Honl, where I is the current that runs through the solenoid, and n is the number of turns per unit length. Note that the magnetic field of the solenoid does not depend on the radius of the solenoid, in contrast to the magnetic field of a coil. For the experiment in this labatorial, we will use a Slinky. It is not as tightly wound as a solenoid should be, but that gives us the chance to conveniently put a magnetic field probe at various points inside the coil. DC power multimeter supply computer probe slinky