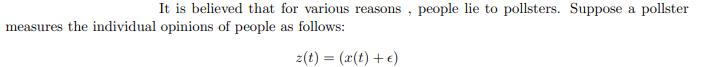
It is believed that for various reasons. people lie to pollsters. Suppose a pollster measures the individual opinions of people as follows: z(t) = (x(t) + ) Here = (1, 2,..., n) is a vector of individual biases, i.e., the extent to which people are lying to the pollster. The pollster does not know this bias beforehand. However, the pollster is quite sure that they understand the propagation of opinions via A. (a) (10 pts) The pollster is confident that the individuals are only lying in the poll, but not to each other. Thus, they can figure out bias by leveraging their model of propagation. Show why this is so by giving a linear algebraic expression for e in terms of two consecutive measurements. No numerical evaluation is needed, leave your answer in terms of an expression. (b) (10 pts) Suppose the situation is more complicated, because people are in fact mis-representing their opinions to each other. Thus, propagation proceeds via: r(t+1) = A (r(t)+7), where y is a bias associated with mis-representation of opinions to others. Is it now possible to determine both biases, and y? Characterize as completely and generally as possible. Again, no numerics are needed here.