ITBP301 Security Principles and Practices

Lab#2: ASYMMETRIC ENCRYPTION

Objectives

Giving you hands-on experience with RSA algorithm and the RSA key generation process.

Overview: Public-Key Cryptographic Algorithm (Asymmetric) and RSA

In symmetric encryption, a single key is used to both encrypt plaintext and decrypt ciphertext, as explained in the previous lab. The key is typically a large number that is used to mathematically transform the message. The problem then becomes the secure distribution of the symmetric key itself. This is known as the key management problem.

To solve the key management problem, two different keys are used one is public used for encryption and the other is private used for decryption. For example, if Alice and Bob want to communicate securely. Alice could then send her public key to Bob, who could use it to send an encrypted message back to Alice. Provided Alice keeps her private key, no one will be able to decrypt it other than Alice herself. For this reason, this type of system is called a public-key encryption system. Therefore, the encryption key is called the public key, and the decryption key is called the private key.

Simply put, the Symmetric Key Algorithm works similar to a keyed lock, and the Asymmetric Key Algorithm works like a combination lock.

In this lab, you will be working with a simplified and not very secure version of one of the most popular public-key systems: the RSA public-key encryption system Like all public-key systems, the keys are derived using a trapdoor operation an operation that is easy to do but difficult to undo. In RSA, this operation is the multiplication of two large prime numbers: it is easy and fast to multiply the two numbers together, but it is significantly more difficult and time consuming to factor the resulting number back into its prime components. In this lab experience, you will be using relatively small primes (only three digits) to see how this system works.

RSA Algorithm:

To explore this system in more depth, you will be exchanging encrypted messages with a partner. Choose your partner now.

Lab Tasks

1. Launch Microsoft Excel provided with this exercise and open the spreadsheet

   You may see a warning message informing you that the workbook contains macros. Since you will not need these macros to use the workbook (they are left over from an older and less efficient version of this lab), click on the Disable Macros button.

2. This spreadsheet makes use of some specialized functions that are not part of the standard function set in Microsoft Excel. However, they are included in an extra set of functions called the Analysis Toolpak. Click on File > Options > Add-Ins. At the bottom of the window, you will see Manage: Excel Add-Ins. Click Go... In the dialogue box that appears, click on the check box to the left of the entry Analysis Toolpak. When a checkmark appears, click on OK.

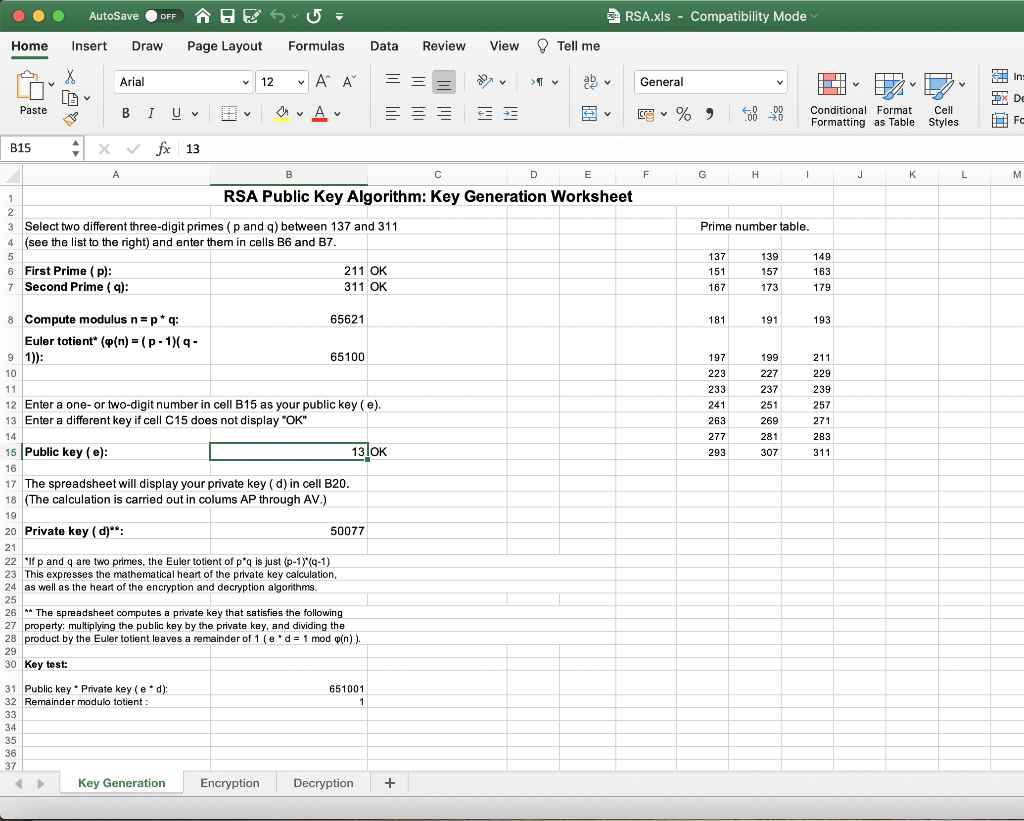
3. If necessary, click on the tab for the Key Generation worksheet. Use a random process to choose two different prime numbers p and q between 137 and 311 (displayed in a list in cells G5:I15). Enter these primes in cells B6 and B7. Be sure that cells C6 and C7 both display the message OK. The spreadsheet automatically computes the modulus (the product p*q) in cell B8 and the Euler totient (the product (p-1)*(q-1)) in cell B9. Note that the Euler totient would be difficult to determine from the modulus by itself; one needs to know the two primes. Write your two primes, your modulus, and your Euler totient below:

p: q: modulus:

Euler totient:

4. Choose a small number (no more than two digits) that has no factors (except 1) in common with the Euler totient. Enter this number as your public key in cell B15. If cell C15 displays the message Invalid Public Key, you need to select a different public key. When you have chosen a valid public key, the message OK will appear in cell C15. The spreadsheet will automatically compute your private key in cell B20. The private key is chosen so that (Public Key)*(Private Key) leaves a remainder of one when divided by the Euler totient. (This would not be possible if the private had a factor other than 1 in common with the Euler totient.) Write your public and private keys below:

   Public key:

   Private key:

5. Once both you and your partner have each created a modulus and pair of keys, you are ready to exchange encrypted messages. Give your modulus and public

key to your partner. Do not give your partner your private key or Euler totient. In return, your partner will give you her/his public key and modulus.

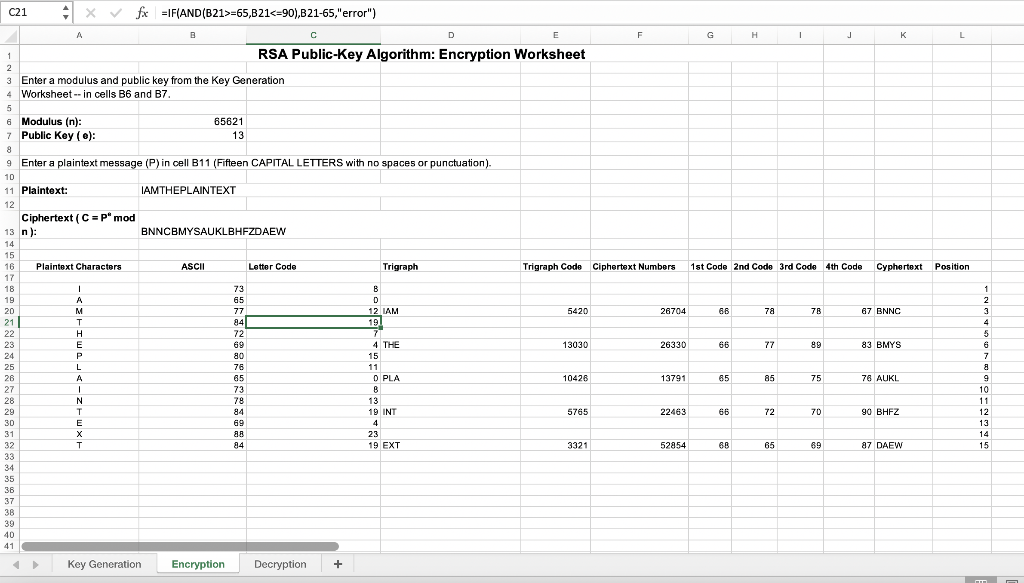
6. Click on the tab for the Encryption worksheet. Enter your partners modulus and public key in cells B6 and B7. Write these values below:

   Partners modulus:

   Partners public key:

7. Enter a message in cell B11. This message should consist of a string of fifteen or more capital letters with no spaces or punctuation marks. The spreadsheet will encipher only the first fifteen letters of your message. Your message could be a short phrase or sentence. For example, PLEASEHELPMENOW to test this spreadsheet. Note that a message to be enciphered is usually called plaintext. The enciphered form of the message is called the cipher text.

8. The enciphered form of the message (the cipher text) should appear in cell B13. (This may take a few seconds.) The spreadsheet determines the ciphertext as follows:

   • Split the plaintext up into blocks of three letters (called trigraphs).

   • Obtain a numeric representation for each letter based on its position in the

     alphabet (A0, b1, etc.).

   • Compute a numeric code for each trigraph using the formula

     (First Letter Code) * 26^2 + (Second Letter Code) * 26 + (Third Letter code).

   • For the mathematically inclined, this is interpreting each trigraph as a number in base twenty-six.

   • Encipher each plaintext trigraph code by computing (Plaintext

     Public Key

trigraph code)

, dividing the result by the Modulus and taking the

remainder.

• Convert each enciphered trigraph code into a quadragraph a block of four

  letters as follows:

• Divide the code by 26^3. The quotient is the code for the first letter of the

  quadragraph. The spreadsheet uses the remainder to get codes for the other

  three letters.

• Divide the remainder from the first step by 26^2. The quotient is the code

  for the second letter. The spreadsheet uses the remainder to get the codes for

  the other two letters.

• Divide the remainder from the second step by 26. The quotient is the code

  for the third letter and the remainder is the code for the fourth letter.

• For the mathematically inclined, this quadragraph calculation determines the representation of the enciphered message as a four-digit number in base

  twenty-six (using the letters of the alphabet as our digits).

• Some of the details of this calculation appear in cells A16:K38 of the Encoding worksheet. Enter the plaintext and ciphertext below. Show the

  steps of the conversion process in the table. Plaintext:

Ciphertext:

9. Give the ciphertext (but not the plaintext) to your partner. In return, your partner will give you a ciphertext message. Record the ciphertext message from your partner below. In the rest of this exercise, you will be deciphering this message.

   Ciphertext from partner:

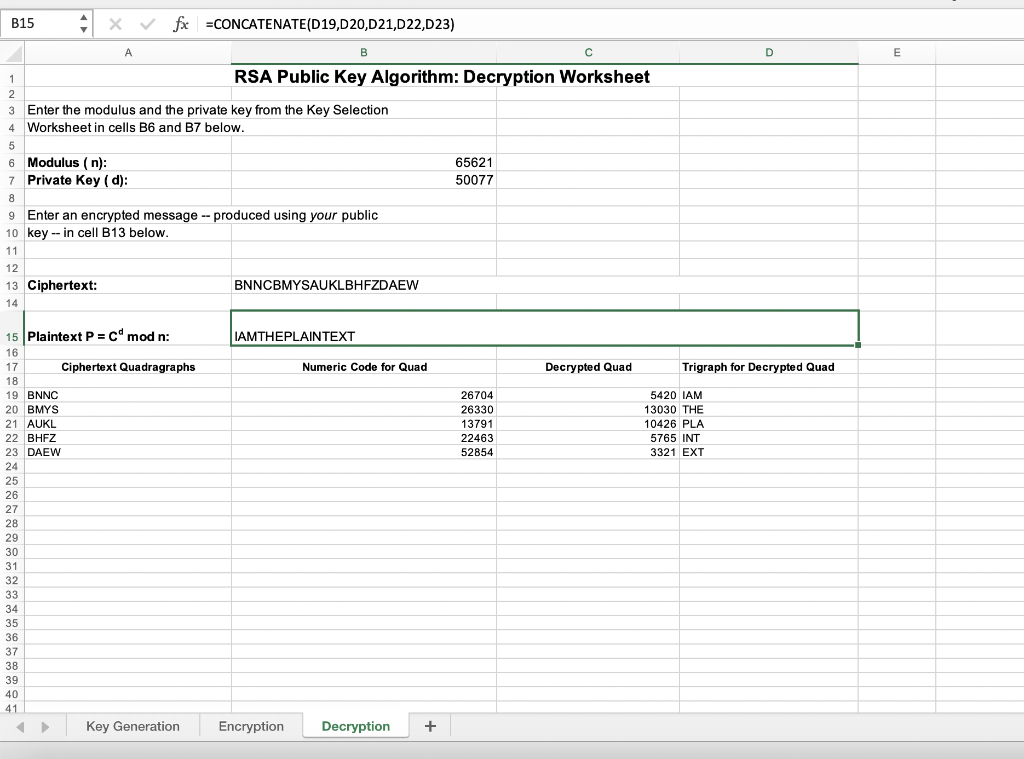
10. Click on the tab for the Decryption worksheet. Enter your modulus and your private key in cells B6 and B7 of this worksheet. Enter the cipher text you received from your partner as the Encrypted Message in cell B13. The deciphering process is similar to the enciphering process:

    • Split the ciphertext up into quadragraphs (instead of trigraphs).

    • Obtain the numeric representation for each letter and compute a numeric

      code for each trigraph using the formula

      (First Letter Code) * 26^3 + (Second Letter Code) * 26^2 + (Third Letter

      Code) * 26 + (Fourth Letter Code). Encipher each ciphertext quadragraph code by computing (Ciphertext

      Private Key

quadragraph code)

, dividing the result by the Modulus and taking

the remainder Convert each deciphered quadragraph code into a trigraph.

1. Divide the code by 26^2. The quotient is the code for the first letter.

2. Divide the remainder from the first step by 26. The quotient will be the code for the second letter and the remainder the code for the third.

Note that deciphering uses the private key in place of the public key. Some of the details of this calculation appear in cells A19:D23 of the Decoding Worksheet. The deciphered message should appear in cell B13. Record the results of each deciphering step in the table below.

Now, write the deciphered message (plaintext) below. Deciphered message:

Attacks on RSA

One of the most common attacks on RSA is prime factorization attack.

Example: The following cipher text is encrypted using a weak RSA key whose modulus and public exponent are given below. Crack the private key and decrypt the cipher text.

Cipher Text:

90505123045132495707756134797 # 83941985085686243344731117726 # 77041600692822724019390698270 # 84377920180551736810404465769 # 23298631191590239622004976020 # 76044851276011511729119265079

Modulus N = 106098117893828030018249920531 Public Exponent e = 2^16+1

Hybrid Encryption: RSA-AES Encryption Asymmetric Encryption is usually implemented in combination with symmetric methods. This is known as hybrid encryption. It consists of 1. Generation of a random symmetric key (session key) 2. Session key is transferred protected by asymmetric key 3. Message is encrypted by the session key

Follow the steps on the flow chart and you will end up with an encrypted message as shown on the figure. The whole message consists of the public key used to encrypt the session key, the encrypted session key and the encrypted message.

AutoSave OFF BESU- RSA.xls - Compatibility Mode Home Insert Draw Page Layout Formulas Data Review View Tell me X Arial 12 A General In: y Paste av A v + y % 8 .00 > Conditional Format Formatting as Table X DO ! Fc Cell Styles B F G H 1 L M B15 fx 13 A E RSA Public Key Algorithm: Key Generation Worksheet 3 Select two different three-digit primes (p and q) between 137 and 311 4 (see the list to the right) and enter them in cells B6 and B7. 5 6 First Prime (p): 211 OK 7 Second Prime (a): 311 OK 1 2 Prime number table. 137 151 167 139 157 149 163 173 179 181 191 193 197 211 229 223 233 241 263 199 227 237 251 269 239 257 271 277 281 283 293 307 311 8 Compute modulus n=p* q: 65621 Euler totient ((n) = (p-1)- 9 1)) 65100 10 11 12 Enter a one-or two-digit number in cell B15 as your public key (e). 13 Enter a different key if cell C15 does not display "OK" 14 15 Public key (e): 13.OK 16 17 The spreadsheet will display your private key (d) in cell B20. 18 (The calculation is carried out in colums AP through AV.) 19 19 20 Private key (d)**: 50077 21 22 *if p and q are two primes, the Euler totient of pq is just (p-1) (-1) 23 This expresses the mathematical heart of the private key calculation, 24 as well as the heart of the encryption and decryption algorithms 25 26 ** The spreadsheet computes a private key that satisfies the following 27 property: multiplying the public key by the private key, and dividing the 28 product by the Euler totient leaves a remainder of 1 (e* d = 1 mod o(n)). 29 30 Key test: 651001 1 31 Public key Private key (ed); 32 Remainder modulo totient : 33 34 35 36 37 Key Generation Encryption Decryption + C21 x fx =IF(AND(B21>=65,B21 Conditional Format Formatting as Table X DO ! Fc Cell Styles B F G H 1 L M B15 fx 13 A E RSA Public Key Algorithm: Key Generation Worksheet 3 Select two different three-digit primes (p and q) between 137 and 311 4 (see the list to the right) and enter them in cells B6 and B7. 5 6 First Prime (p): 211 OK 7 Second Prime (a): 311 OK 1 2 Prime number table. 137 151 167 139 157 149 163 173 179 181 191 193 197 211 229 223 233 241 263 199 227 237 251 269 239 257 271 277 281 283 293 307 311 8 Compute modulus n=p* q: 65621 Euler totient ((n) = (p-1)- 9 1)) 65100 10 11 12 Enter a one-or two-digit number in cell B15 as your public key (e). 13 Enter a different key if cell C15 does not display "OK" 14 15 Public key (e): 13.OK 16 17 The spreadsheet will display your private key (d) in cell B20. 18 (The calculation is carried out in colums AP through AV.) 19 19 20 Private key (d)**: 50077 21 22 *if p and q are two primes, the Euler totient of pq is just (p-1) (-1) 23 This expresses the mathematical heart of the private key calculation, 24 as well as the heart of the encryption and decryption algorithms 25 26 ** The spreadsheet computes a private key that satisfies the following 27 property: multiplying the public key by the private key, and dividing the 28 product by the Euler totient leaves a remainder of 1 (e* d = 1 mod o(n)). 29 30 Key test: 651001 1 31 Public key Private key (ed); 32 Remainder modulo totient : 33 34 35 36 37 Key Generation Encryption Decryption + C21 x fx =IF(AND(B21>=65,B21