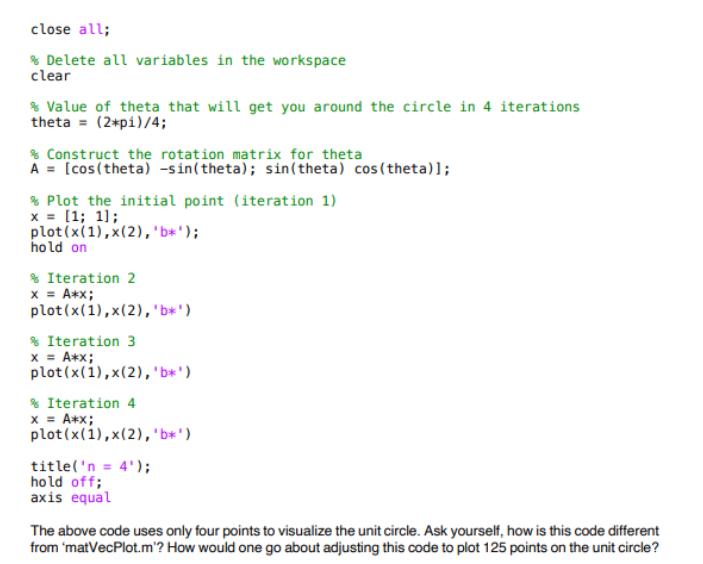
Iteration is the repetition of the same process over and over again. It is a crucial programming tool that we will get some practice using this week. To get started, lets recall matrix-vector multiplication. In two dimensions, matrix-vector multiplication is computed according to the following process: which can be written simply as: where x and y are 2-by-1 vectors: and A is a 2-by-2 matrix: y(1) = A(1,1) x(1) + A(1,2) = x(2) y(2) = A(2,2) x(2) + A(2,2)=x(2) A [0 1; -1 0]; x = [1; 1]; y = A *x x=[x2], x=[2] X= y [A(1,1) A(1,2)] A(2,1) A(2,2) Let's examine the effect of iterating matrix-vector multiplication with A=13 Create a Matlab script entitled 'matVecPlot.m' to run the following code: y = A*x; plot ( [0 x(1)],[0 x(2)]); hold on plot([0 y(1)],[0 y(2)], 'r'); y = A*y; plot ( [0 y(1)], [0 (2)],"g-'); y = A*y; plot ( [@ y(1)], 10 y(2)], 'y-.'); axis equal Once you get it working, examine what the code is doing. Practice thoroughly commenting your script to describe what it does (in the header) and what each line of code is doing. Check out coinFlipping.m to see an example. Problem 1: A rotation matrix has the general form: [cos (0) (sin(0) A -sin (0)] si cos(0) where defines the angle of rotation. For example, setting = yields the matrix we employed in matVecPlot.m (try it, just to be sure). We will now use a rotation matrix to visualize the unit circle. Let's start by altering our existing script: Make sure there are no other figures open close all; % Delete all variables in the workspace clear & Value of theta that will get you around the circle in 4 iterations theta = (2*pi)/4; & Construct the rotation matrix for theta A = [cos (theta) -sin(theta); sin (theta) cos (theta)]; & Plot the initial point (iteration 1) x = [1; 1]; plot (x (1),x(2), 'b*'); hold on * Iteration 2 x = A*x; plot(x(1),x(2), 'b*') % Iteration 3 x = A*x; plot (x (1), x(2), 'b*') % Iteration 4 plot(x(1),x(2), 'b*') title('n = 4'); hold off; axis equal The above code uses only four points to visualize the unit circle. Ask yourself, how is this code different from 'matVecPlot.m'? How would one go about adjusting this code to plot 125 points on the unit circle? Generalize the above code to create a function unitCircle.m that plots n points on the unit circle (use a for-loop). Be sure to include a header, thorough comments, proper code indentation, and incorporate an informative title to your plot that includes your name. Tum in a a plot for n = 125. Problem 2: Grow a Fern In Problem 1, we used a rotation matrix to visualize the unit circle. In this problem, we will grow a fern using more general affine transformations: y = A *x + b where b is a 2-by-1 vector that "shifts" the positions of A*x. Affine transformations can encode rotation, stretching, and shifting (assuming A is invertible, but don't worry about that now), and despite their simplicity, are used in many important applications. Here's a very well-known and interesting example from brain image analysis: https://www.sciencedirect.com/science/article/pii/S1361841501000366?via%3Dihub We are going to mathematically model our fern with a fractal and use a simple Iterated Function System: https://en.wikipedia.org/wiki/lterated function system. Though I'm sure we would all greatly enjoy delving into the mathematics behind fractals, for this exercise, we only need to write a code that iteratively grows the fern. Specifically, for each iteration, your code fern.m should generate a random number and Apply x = [0 0;0 0.16]** Apply x = [0.85 0.04; -0.04 0.85]*x + [0; 1.6] Apply x = [0.2 -0.26; 0.23 0.22] *x + [0; 1.61; Apply x = [-0.15 0.28; 0.26 0.24] *x + [0; 0.44]; with probability p = 0.07 with probability p = 0.01 with probability p = 0.85 with probability p = 0.07 Initialize your iteration with x = [0; 0)] and run the iteration for n = 2750 times. Be sure to include a header, thoroughly comment your code, and incorporate an informative title to your plot. Note that the fern iteration involves four conditions. Your code should make use of the elseif statement to handle these conditions. Figure 1: An example fern created with 5000 points Problem 1 o 'unitCircle.m' Fully commented code Proper Indentation Correct use of for-loop Correct output plot for n = 125 Problem 2 o'fern.m' . Fully commented code Proper indentation . Correct use of elseif statement Correct output plot