Java Class:

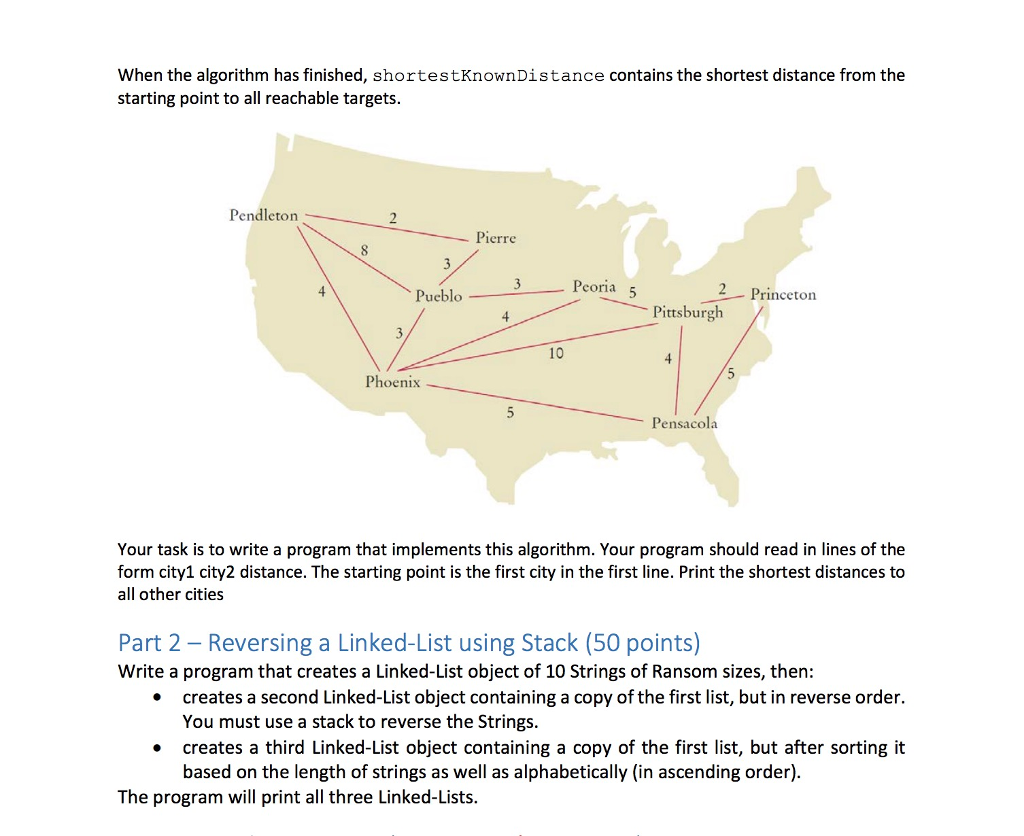
Part 1 - Finding Least Expensive Routes (50 points) Consider the problem of finding the least expensive routes to all cities in a network from a given starting point. For example, in the network shown on the map below, the least expensive route from Pendleton to Peoria has cost 8 (going through Pierre and Pueblo) The following helper class expresses the distance to another city: public class DistanceTo implements Comparable private String target private int distance; public DistanceTo (String city, int dist) targetcity; distance -dist: public String getTarget) return target; public int getDistance ) return distance; public int compareTo (DistanceTo other) return distance - other.distance; All direct connections between cities are stored in a Map?String, TreeSet> The algorithm now proceeds as follows: Let from be the starting point Add DistanceTo(from, 0) to a priority queue. Construct a map shortestKnownDistance from city names to distances. While the priority queue is not empty Get its smallest element If its target is not a key in shortestKnownDistance Let d be the distance to that target. Put (target, d) into shortestKnownDistance. For all cities c that have a direct connection from target Add DistanceTo(c, d + distance from target to c) to the priority queue. Part 1 - Finding Least Expensive Routes (50 points) Consider the problem of finding the least expensive routes to all cities in a network from a given starting point. For example, in the network shown on the map below, the least expensive route from Pendleton to Peoria has cost 8 (going through Pierre and Pueblo) The following helper class expresses the distance to another city: public class DistanceTo implements Comparable private String target private int distance; public DistanceTo (String city, int dist) targetcity; distance -dist: public String getTarget) return target; public int getDistance ) return distance; public int compareTo (DistanceTo other) return distance - other.distance; All direct connections between cities are stored in a Map?String, TreeSet> The algorithm now proceeds as follows: Let from be the starting point Add DistanceTo(from, 0) to a priority queue. Construct a map shortestKnownDistance from city names to distances. While the priority queue is not empty Get its smallest element If its target is not a key in shortestKnownDistance Let d be the distance to that target. Put (target, d) into shortestKnownDistance. For all cities c that have a direct connection from target Add DistanceTo(c, d + distance from target to c) to the priority queue