java

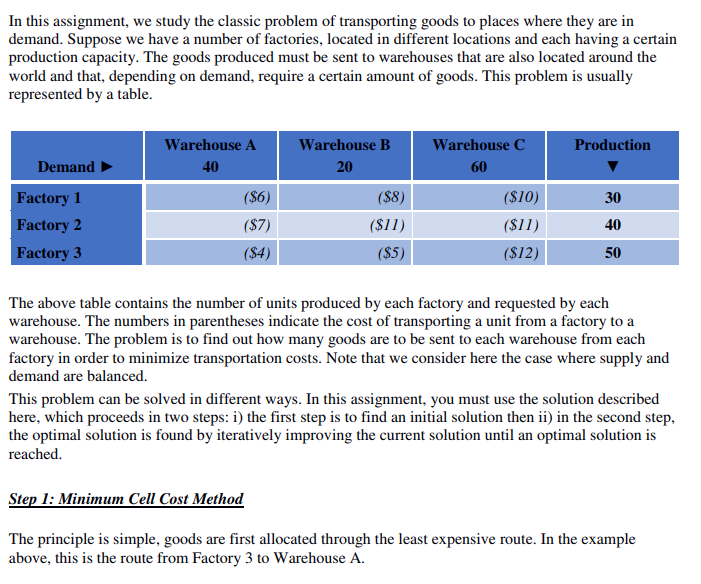
In this assignment, we study the classic problem of transporting goods to places where they are in demand. Suppose we have a number of factories, located in different locations and each having a certain production capacity. The goods produced must be sent to warehouses that are also located around the world and that, depending on demand, require a certain amount of goods. This problem is usually represented by a table Warehouse A 40 Warehouse B 20 Warehouse C 60 Production Demand ($6) ($7) ($4) ($8) ($11) (S5 (S10) (S11) ($12 Factory 1 30 40 50 Factory 2 Factory 3 The above table contains the number of units produced by each factory and requested by each warehouse. The numbers in parentheses indicate the cost of transporting a unit from a factory to a warehouse. The problem is to find out how many goods are to be sent to each warehouse from each factory in order to minimize transportation costs. Note that we consider here the case where supply and demand are balanced. This problem can be solved in different ways. In this assignment, you must use the solution described here, which proceeds in two steps: i) the first step is to find an initial solution then ii) in the second step the optimal solution is found by iteratively improving the current solution until an optimal solution is reached. Step 1: Minimum Cell Cost Method The principle is simple, goods are first allocated through the least expensive route. In the example above, this is the route from Factory 3 to Warehouse A. Warehouse A 40 Warehouse B 20 Warehouse C Production Demand Factory 1 Factory 2 Factory 3 (10) 30 40 50 40 (12) The next allocation is made using the least expensive remaining route, knowing that Factory 3 has only 10 units left. Warehouse B 20 Warehouse A Warehouse C Production Demand Factory 1 Factory 2 Factory 3 40 (10) 30 40 50 40 (4 10 (5) (12) The process continues by identifying the next lower cost route by noting that Warehouse A has received all the goods requested (so the cells in the first column can no longer be used) and that Factory 3 has already committed all its goods (so cells in the last row can no longer be used). The next assignment is therefore Warehouse B 20 Warehouse C Warehouse A 40 Production Demand Factory 1 Factory 2 Factory 3 10 (8) (10) 30 40 50 40 10 (5) (12 Which only leaves the demand at warehouse C: Warehouse B 20 Warehouse A Warehouse C Production Demand Factory 1 Factory 2 Factory 3 40 10 (8) 20 (10) 40 (11) (12) 30 40 50 40 (4 10 (5) When all the goods of the factories have been assigned to warehouses, an initial solution is found. However, this solution is not optimal. Some roads are not used. The second step is therefore to determine whether the use of these unused roads would reduce the total cost of transportation. Part 1: Obiect-oriented solution (Lava) [3 marks] Create the classes needed to solve this problem. Your program must be an application called findOptimalTransport that takes the input data file as an argument In addition to the source code, you must also submit a UML class diagram showing all classes, their attributes, methods, and associations. You can not use static methods (except main). Your program must be a Java application that takes as a command line argument the name of the data file. In this assignment, we study the classic problem of transporting goods to places where they are in demand. Suppose we have a number of factories, located in different locations and each having a certain production capacity. The goods produced must be sent to warehouses that are also located around the world and that, depending on demand, require a certain amount of goods. This problem is usually represented by a table Warehouse A 40 Warehouse B 20 Warehouse C 60 Production Demand ($6) ($7) ($4) ($8) ($11) (S5 (S10) (S11) ($12 Factory 1 30 40 50 Factory 2 Factory 3 The above table contains the number of units produced by each factory and requested by each warehouse. The numbers in parentheses indicate the cost of transporting a unit from a factory to a warehouse. The problem is to find out how many goods are to be sent to each warehouse from each factory in order to minimize transportation costs. Note that we consider here the case where supply and demand are balanced. This problem can be solved in different ways. In this assignment, you must use the solution described here, which proceeds in two steps: i) the first step is to find an initial solution then ii) in the second step the optimal solution is found by iteratively improving the current solution until an optimal solution is reached. Step 1: Minimum Cell Cost Method The principle is simple, goods are first allocated through the least expensive route. In the example above, this is the route from Factory 3 to Warehouse A. Warehouse A 40 Warehouse B 20 Warehouse C Production Demand Factory 1 Factory 2 Factory 3 (10) 30 40 50 40 (12) The next allocation is made using the least expensive remaining route, knowing that Factory 3 has only 10 units left. Warehouse B 20 Warehouse A Warehouse C Production Demand Factory 1 Factory 2 Factory 3 40 (10) 30 40 50 40 (4 10 (5) (12) The process continues by identifying the next lower cost route by noting that Warehouse A has received all the goods requested (so the cells in the first column can no longer be used) and that Factory 3 has already committed all its goods (so cells in the last row can no longer be used). The next assignment is therefore Warehouse B 20 Warehouse C Warehouse A 40 Production Demand Factory 1 Factory 2 Factory 3 10 (8) (10) 30 40 50 40 10 (5) (12 Which only leaves the demand at warehouse C: Warehouse B 20 Warehouse A Warehouse C Production Demand Factory 1 Factory 2 Factory 3 40 10 (8) 20 (10) 40 (11) (12) 30 40 50 40 (4 10 (5) When all the goods of the factories have been assigned to warehouses, an initial solution is found. However, this solution is not optimal. Some roads are not used. The second step is therefore to determine whether the use of these unused roads would reduce the total cost of transportation. Part 1: Obiect-oriented solution (Lava) [3 marks] Create the classes needed to solve this problem. Your program must be an application called findOptimalTransport that takes the input data file as an argument In addition to the source code, you must also submit a UML class diagram showing all classes, their attributes, methods, and associations. You can not use static methods (except main). Your program must be a Java application that takes as a command line argument the name of the data file