Java Language
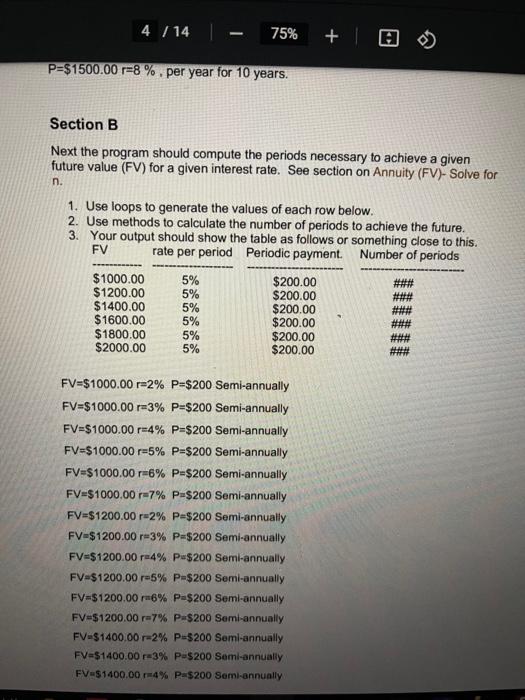
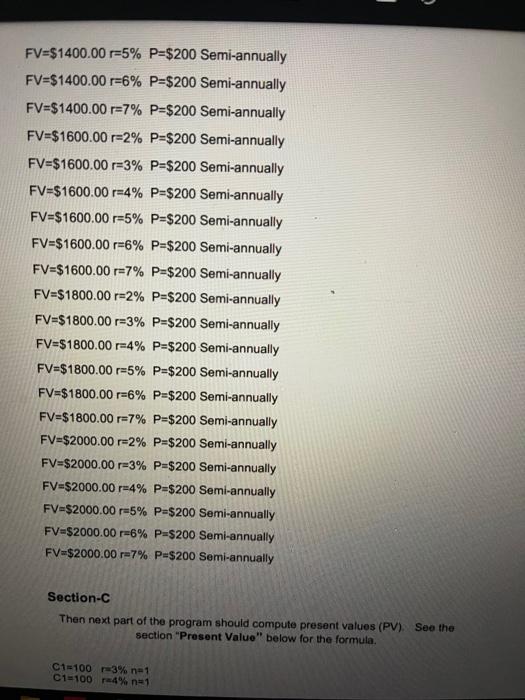
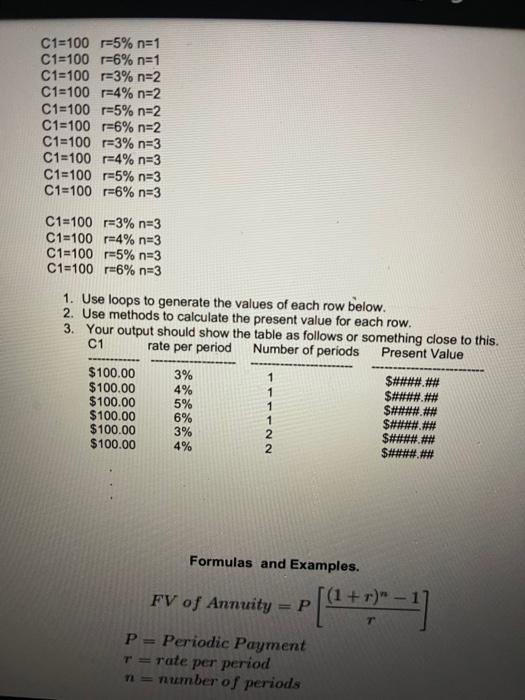
Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods. Do sections A B and C in one program Section A With the below inputs compute and display the future value of an annuity and the future value with continuous compounding. Also display the difference in the future value with continuous compounding and the future value. Your program should 1. Use loops to generate the values of each row below. 2. Use methods to calculate the Future Value and the future value with continuous compounding, 3. Your output should display your name and Student Number 4. Your output should show the table as follows or something close to this. Payment APR Years FV FV/Continuous FVIC - FV $500.00 $500.00 $500.00 $500.00 2 % 3 % 4 % 5 % on or on on $####.## $####.## $####.## $####.## $####.## $####.## $####.## $###### S###### $###### $###### S####.## P=$500.00 r=2 %, per year for 5 years. P=$500.00 3% . per year for 5 years. P=$500.00 24 %. per year for 5 years. P=$500.00 r=5 %. per year for 5 years. P=$500.00 r=6%. per year for 5 years. Pa$500.00 r=7% per year for 5 years. P=$500.00 -8% per year for 5 years. P-$500.00 r2 %. per year for 7 years. P=$500.00 r3%. per year for 7 years Pu$500.00 24%. per year for 7 years 4 / 14 75% + P=$1500.00 r=8 %. per year for 10 years. Section B Next the program should compute the periods necessary to achieve a given future value (FV) for a given interest rate. See section on Annuity (FV)- Solve for n. 1. Use loops to generate the values of each row below. 2. Use methods to calculate the number of periods to achieve the future. 3. Your output should show the table as follows or something close to this. FV rate per period Periodic payment. Number of periods 5% 5% $1000.00 $1200.00 $1400.00 $1600.00 $1800.00 $2000.00 5% 5% 5% 5% $200.00 $200.00 $200.00 $200.00 $200.00 $200.00 ### FV=$1000.00 r=2% P=$200 Semi-annually FV=$1000.00 r=3% P=$200 Semi-annually FV=$1000.00 r=4% P=$200 Semi-annually FV=$1000.00 r=5% P=$200 Semi-annually FV=$1000.00 r=6% P=$200 Semi-annually FV=$1000.00 r=7% P=$200 Semi-annually FV=$1200.00 r=2% P-$200 Semi-annually FV=$1200.00 -3% P-$200 Semi-annually FV=$1200.00 -4% P-$200 Semi-annually FV=$1200.00 -5% P=$200 Semi-annually FV=$1200.00 -6% P=$200 Semi-annually FV=$1200.00 -7% P-$200 Semi-annually FV=$1400.00 -2% P-5200 Semi-annually FV=$1400.00 -3% Pu$200 Semi-annually FV-51400.00 -4% Pa$200 Semi-annually FV=$1400.00 r=5% P=$200 Semi-annually FV=$1400.00 r=6% P=$200 Semi-annually FV=$1400.00 r=7% P=$200 Semi-annually FV=$1600.00 r=2% P=$200 Semi-annually FV=$1600.00 r=3% P=$200 Semi-annually FV=$1600.00 r=4% P=$200 Semi-annually FV=$1600.00 r=5% P=$200 Semi-annually FV=$1600.00 r=6% P=$200 Semi-annually FV=$1600.00 r=7% P=$200 Semi-annually FV=$1800.00 r=2% P=$200 Semi-annually FV=$1800.00 r=3% P=$200 Semi-annually FV=$1800.00 -4% P=$200 Semi-annually FV=$1800.00 r=5% P=$200 Semi-annually FV=$1800.00 r=6% P=$200 Semi-annually FV=$1800.00 r=7% P=$200 Semi-annually FV=$2000.00 r=2% P=$200 Semi-annually FV=$2000.00 -3% P=$200 Semi-annually FV=$2000.00 r=4% P=$200 Semi-annually FV=$2000.00 -5% P=$200 Semi-annually FV=$2000.00 -6% P=$200 Semi-annually FV=$2000.00 -7% P=$200 Semi-annually Section- Then next part of the program should compute present values (PV). See the section "Present Value' below for the formula C1=100 -3% n=1 C1=100 -4% n=1 C1=100 =5% n=1 C1=100 r=6% n=1 C1=100 =3% n=2 C1=100 r=4% n=2 C1=100 r=5% n=2 C1=100 r=6% n=2 C1=100 =3% n=3 C1=100 =4% n=3 C1=100 =5% n=3 C1=100 r=6% n=3 C1=100 =3% n=3 C1=100 r=4% n=3 C1=100 =5% n=3 C1=100 r=6% n=3 1. Use loops to generate the values of each row below. 2. Use methods to calculate the present value for each row. 3. Your output should show the table as follows or something close to this. C1 rate per period Number of periods Present Value 1 1 $100.00 $100.00 $100.00 $100.00 $100.00 $100.00 3% 4% 5% 6% 3% 4% 1 $###### $#*##.## $####.## $###### $####.## $###### NN Formulas and Examples. (1+ FV of Annuity P P = Periodic Payment T=rate per period n = number of periods Compounding Derived? The future value of annuity with continuous compounding formula is the sum of future cash flows with interest. The sum of cash flows with continuous compounding can be shown as = CF(e)" +CF(e)?r...CF(e)" This is considered a geometric series as the cash flows are all equal. The common ratio for this example is er. The geometric series formula for the formula above shows = CF (1 - e) (1 - e) The entire formula above can be multiplied by -1/-1 to get the formula originally given. Annuity (FV)- Solve for n NFVA = In = In (1+ "VX") = ln(1+r) n = number of periods FV = Future Value (of Annuity) r=rate P= Payment/Cash Flows The formula for solving for number of periods (n) on an annuity shown above is used to calculate the number of periods based on the future value, rate, and periodic cash flows. The formula above, solving for n, generally approaches the question "How long will it take to save $x amount dollars by saving $y per month at a rate of z%". Example of Solve for n on Annuity Formula Suppose that an individual receives an additional $1000 pay or bonus semiannually. Suppose this individual would like to find out how long until they save $19600 by saving $1,000 every half year at an effective rate of 5% every half year. **It is important to remember that the rate should match the frequency of the cash flows/payments. For example, if cash flows are semi- annual, then the effective semi-annual rate is used. The term effective implies that compounding is already adjusted for that period (see effective rate). Using the formula at the top of the page to solve for the number of periods, n, for this example would show the equation The above equation can be reduced to = In(1.98) In(1.05) which results in 14 semi-annual periods. Present Value C PV = (1 + r)" Ci=Cash Flow at period 1 r=rate of return n = number of periods Present Value (PV) is a formula used in Finance that calculates the present day value of an amount that is received at a future date. The premise of the equation is that there is "time value of money". Time value of money is the concept that receiving something today is worth more than receiving the same item at a future date. The presumption is that it is preferable to receive $100 today than it is to receive the same amount one year from today, but what if the choice is between $100 present day or $106 a year from today? A formula is needed to provide a quantifiable comparison between an amount today and an amount at a future time, in terms of its present day value. Use of Present Value Formula The Present Value formula has a broad range of uses and may be applied to various areas of finance including corporate finance, banking finance, and investment finance. Apart from the various areas of finance that present value analysis is used, the formula is also used as a component of other financial formulas. Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods. Do sections A B and C in one program Section A With the below inputs compute and display the future value of an annuity and the future value with continuous compounding. Also display the difference in the future value with continuous compounding and the future value. Your program should 1. Use loops to generate the values of each row below. 2. Use methods to calculate the Future Value and the future value with continuous compounding, 3. Your output should display your name and Student Number 4. Your output should show the table as follows or something close to this. Payment APR Years FV FV/Continuous FVIC - FV $500.00 $500.00 $500.00 $500.00 2 % 3 % 4 % 5 % on or on on $####.## $####.## $####.## $####.## $####.## $####.## $####.## $###### S###### $###### $###### S####.## P=$500.00 r=2 %, per year for 5 years. P=$500.00 3% . per year for 5 years. P=$500.00 24 %. per year for 5 years. P=$500.00 r=5 %. per year for 5 years. P=$500.00 r=6%. per year for 5 years. Pa$500.00 r=7% per year for 5 years. P=$500.00 -8% per year for 5 years. P-$500.00 r2 %. per year for 7 years. P=$500.00 r3%. per year for 7 years Pu$500.00 24%. per year for 7 years 4 / 14 75% + P=$1500.00 r=8 %. per year for 10 years. Section B Next the program should compute the periods necessary to achieve a given future value (FV) for a given interest rate. See section on Annuity (FV)- Solve for n. 1. Use loops to generate the values of each row below. 2. Use methods to calculate the number of periods to achieve the future. 3. Your output should show the table as follows or something close to this. FV rate per period Periodic payment. Number of periods 5% 5% $1000.00 $1200.00 $1400.00 $1600.00 $1800.00 $2000.00 5% 5% 5% 5% $200.00 $200.00 $200.00 $200.00 $200.00 $200.00 ### FV=$1000.00 r=2% P=$200 Semi-annually FV=$1000.00 r=3% P=$200 Semi-annually FV=$1000.00 r=4% P=$200 Semi-annually FV=$1000.00 r=5% P=$200 Semi-annually FV=$1000.00 r=6% P=$200 Semi-annually FV=$1000.00 r=7% P=$200 Semi-annually FV=$1200.00 r=2% P-$200 Semi-annually FV=$1200.00 -3% P-$200 Semi-annually FV=$1200.00 -4% P-$200 Semi-annually FV=$1200.00 -5% P=$200 Semi-annually FV=$1200.00 -6% P=$200 Semi-annually FV=$1200.00 -7% P-$200 Semi-annually FV=$1400.00 -2% P-5200 Semi-annually FV=$1400.00 -3% Pu$200 Semi-annually FV-51400.00 -4% Pa$200 Semi-annually FV=$1400.00 r=5% P=$200 Semi-annually FV=$1400.00 r=6% P=$200 Semi-annually FV=$1400.00 r=7% P=$200 Semi-annually FV=$1600.00 r=2% P=$200 Semi-annually FV=$1600.00 r=3% P=$200 Semi-annually FV=$1600.00 r=4% P=$200 Semi-annually FV=$1600.00 r=5% P=$200 Semi-annually FV=$1600.00 r=6% P=$200 Semi-annually FV=$1600.00 r=7% P=$200 Semi-annually FV=$1800.00 r=2% P=$200 Semi-annually FV=$1800.00 r=3% P=$200 Semi-annually FV=$1800.00 -4% P=$200 Semi-annually FV=$1800.00 r=5% P=$200 Semi-annually FV=$1800.00 r=6% P=$200 Semi-annually FV=$1800.00 r=7% P=$200 Semi-annually FV=$2000.00 r=2% P=$200 Semi-annually FV=$2000.00 -3% P=$200 Semi-annually FV=$2000.00 r=4% P=$200 Semi-annually FV=$2000.00 -5% P=$200 Semi-annually FV=$2000.00 -6% P=$200 Semi-annually FV=$2000.00 -7% P=$200 Semi-annually Section- Then next part of the program should compute present values (PV). See the section "Present Value' below for the formula C1=100 -3% n=1 C1=100 -4% n=1 C1=100 =5% n=1 C1=100 r=6% n=1 C1=100 =3% n=2 C1=100 r=4% n=2 C1=100 r=5% n=2 C1=100 r=6% n=2 C1=100 =3% n=3 C1=100 =4% n=3 C1=100 =5% n=3 C1=100 r=6% n=3 C1=100 =3% n=3 C1=100 r=4% n=3 C1=100 =5% n=3 C1=100 r=6% n=3 1. Use loops to generate the values of each row below. 2. Use methods to calculate the present value for each row. 3. Your output should show the table as follows or something close to this. C1 rate per period Number of periods Present Value 1 1 $100.00 $100.00 $100.00 $100.00 $100.00 $100.00 3% 4% 5% 6% 3% 4% 1 $###### $#*##.## $####.## $###### $####.## $###### NN Formulas and Examples. (1+ FV of Annuity P P = Periodic Payment T=rate per period n = number of periods Compounding Derived? The future value of annuity with continuous compounding formula is the sum of future cash flows with interest. The sum of cash flows with continuous compounding can be shown as = CF(e)" +CF(e)?r...CF(e)" This is considered a geometric series as the cash flows are all equal. The common ratio for this example is er. The geometric series formula for the formula above shows = CF (1 - e) (1 - e) The entire formula above can be multiplied by -1/-1 to get the formula originally given. Annuity (FV)- Solve for n NFVA = In = In (1+ "VX") = ln(1+r) n = number of periods FV = Future Value (of Annuity) r=rate P= Payment/Cash Flows The formula for solving for number of periods (n) on an annuity shown above is used to calculate the number of periods based on the future value, rate, and periodic cash flows. The formula above, solving for n, generally approaches the question "How long will it take to save $x amount dollars by saving $y per month at a rate of z%". Example of Solve for n on Annuity Formula Suppose that an individual receives an additional $1000 pay or bonus semiannually. Suppose this individual would like to find out how long until they save $19600 by saving $1,000 every half year at an effective rate of 5% every half year. **It is important to remember that the rate should match the frequency of the cash flows/payments. For example, if cash flows are semi- annual, then the effective semi-annual rate is used. The term effective implies that compounding is already adjusted for that period (see effective rate). Using the formula at the top of the page to solve for the number of periods, n, for this example would show the equation The above equation can be reduced to = In(1.98) In(1.05) which results in 14 semi-annual periods. Present Value C PV = (1 + r)" Ci=Cash Flow at period 1 r=rate of return n = number of periods Present Value (PV) is a formula used in Finance that calculates the present day value of an amount that is received at a future date. The premise of the equation is that there is "time value of money". Time value of money is the concept that receiving something today is worth more than receiving the same item at a future date. The presumption is that it is preferable to receive $100 today than it is to receive the same amount one year from today, but what if the choice is between $100 present day or $106 a year from today? A formula is needed to provide a quantifiable comparison between an amount today and an amount at a future time, in terms of its present day value. Use of Present Value Formula The Present Value formula has a broad range of uses and may be applied to various areas of finance including corporate finance, banking finance, and investment finance. Apart from the various areas of finance that present value analysis is used, the formula is also used as a component of other financial formulas
