java

package ch11.sorts;

import java.util.*; import java.text.DecimalFormat;

public class Sorts { static final int SIZE = 50; // size of array to be sorted static int[] values = new int[SIZE]; // values to be sorted

static void initValues() // Initializes the values array with random integers from 0 to 99. { Random rand = new Random(); for (int index = 0; index

static public boolean isSorted() // Returns true if the array values are sorted and false otherwise. { for (int index = 0; index values[index + 1]) return false; return true; }

static public void swap(int index1, int index2) // Precondition: index1 and index2 are >= 0 and

static public void printValues() // Prints all the values integers. { int value; DecimalFormat fmt = new DecimalFormat("00"); System.out.println("The values array is:"); for (int index = 0; index

///////////////////////////////////////////////////////////////// // // Selection Sort

static int minIndex(int startIndex, int endIndex) // Returns the index of the smallest value in // values[startIndex]..values[endIndex]. { int indexOfMin = startIndex; for (int index = startIndex + 1; index

static void selectionSort() // Sorts the values array using the selection sort algorithm. { int endIndex = SIZE - 1; for (int current = 0; current

///////////////////////////////////////////////////////////////// // // Bubble Sort

static void bubbleUp(int startIndex, int endIndex) // Switches adjacent pairs that are out of order // between values[startIndex]..values[endIndex] // beginning at values[endIndex]. { for (int index = endIndex; index > startIndex; index--) if (values[index]

///////////////////////////////////////////////////////////////// // // Short Bubble Sort

static boolean bubbleUp2(int startIndex, int endIndex) // Switches adjacent pairs that are out of order // between values[startIndex]..values[endIndex] // beginning at values[endIndex]. // // Returns false if a swap was made; otherwise, returns true. { boolean sorted = true; for (int index = endIndex; index > startIndex; index--) if (values[index]

///////////////////////////////////////////////////////////////// // // Insertion Sort

static void insertItem(int startIndex, int endIndex) // Upon completion, values[0]..values[endIndex] are sorted. { boolean finished = false; int current = endIndex; boolean moreToSearch = true; while (moreToSearch && !finished) { if (values[current]

///////////////////////////////////////////////////////////////// // // Merge Sort

static void merge (int leftFirst, int leftLast, int rightFirst, int rightLast) // Preconditions: values[leftFirst]..values[leftLast] are sorted. // values[rightFirst]..values[rightLast] are sorted. // // Sorts values[leftFirst]..values[rightLast] by merging the two subarrays. { int[] tempArray = new int [SIZE]; int index = leftFirst; int saveFirst = leftFirst; // to remember where to copy back while ((leftFirst

static void mergeSort(int first, int last) // Sorts the values array using the merge sort algorithm. { if (first

///////////////////////////////////////////////////////////////// // // Quick Sort

static int split(int first, int last) { int splitVal = values[first]; int saveF = first; boolean onCorrectSide; first++; do { onCorrectSide = true; while (onCorrectSide) // move first toward last if (values[first] > splitVal) onCorrectSide = false; else { first++; onCorrectSide = (first

static void quickSort(int first, int last) { if (first splitVal quickSort(first, splitPoint - 1); quickSort(splitPoint + 1, last); } }

///////////////////////////////////////////////////////////////// // // Heap Sort

static int newHole(int hole, int lastIndex, int item) // If either child of hole is larger than item this returns the index // of the larger child; otherwise it returns the index of hole. { int left = (hole * 2) + 1; int right = (hole * 2) + 2; if (left > lastIndex) // hole has no children return hole; else if (left == lastIndex) // hole has left child only if (item = left child return hole; else // hole has two children if (values[left] = right child if (values[left]

static void reheapDown(int item, int root, int lastIndex) // Precondition: Current root position is "empty". // // Inserts item into the tree and ensures shape and order properties. { int hole = root; // current index of hole int newhole; // index where hole should move to

newhole = newHole(hole, lastIndex, item); // find next hole while (newhole != hole) { values[hole] = values[newhole]; // move value up hole = newhole; // move hole down newhole = newHole(hole, lastIndex, item); // find next hole } values[hole] = item; // fill in the final hole }

static void heapSort() // Sorts the values array using the heap sort algorithm. { int index; // Convert the array of values into a heap. for (index = SIZE/2 - 1; index >= 0; index--) reheapDown(values[index], index, SIZE - 1); // Sort the array. for (index = SIZE - 1; index >=1; index--) { swap(0, index); reheapDown(values[0], 0, index - 1); } }

///////////////////////////////////////////////////////////////// // // Main

public static void main(String[] args) { initValues(); printValues(); System.out.println("values is sorted: " + isSorted()); System.out.println(); // make call to sorting method here (just remove //) // selectionSort(); // bubbleSort(); // shortBubble(); // insertionSort(); // mergeSort(0, SIZE - 1); // quickSort(0, SIZE - 1); // heapSort();

printValues(); System.out.println("values is sorted: " + isSorted()); System.out.println(); } }

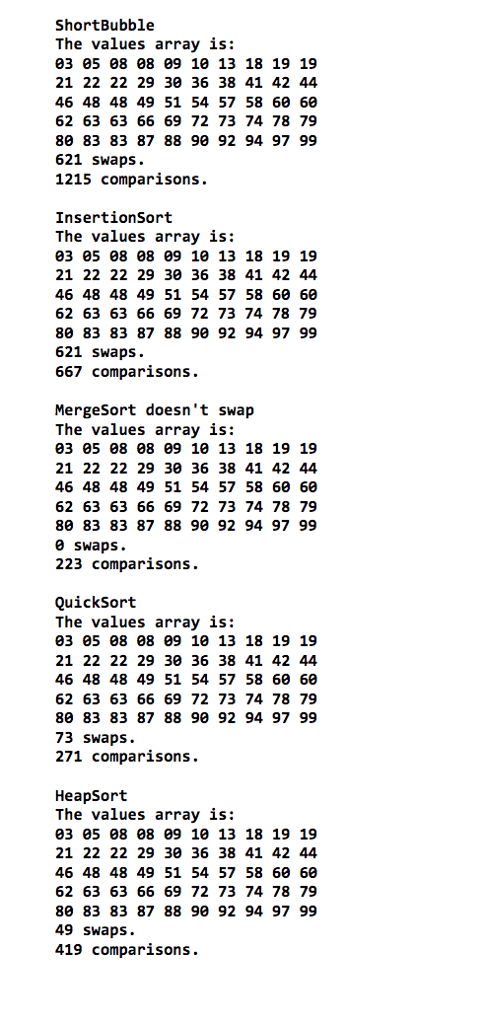
Sorts.java is a test harness program for testing various sorting methods. The program includes a swap method that is used by all of the sorting methods to swap array elements a) Modify the program so that after calling a sorting method the program prints out the number of swaps required to sort an array of 50 random integers b) Test the modified program by running the selectionSort, bubbleSorit, shortBubble, insertionSort, mergeSort, heapSort,and quickSort c) Modify the program so that after calling a sorting method the program prints out the number of comparisons required to sort an array of 50 random integers d) Test the modified program by running the selectionSort, bubbleSort, shortBubble, insertionSort, mergeSort, heapSort, and quickSort e) In order to run the program just once, a backupValues array can be used in the initValues method. Use it to save all of the random numbers assigned to the values array. Then, create a resetValues method to reset the values array back to the original values by using the backupValues array each time you call one of the sorting methods. Of course, the backup array doesn't need to be reset for the first call to a sort-just the subsequent calls to the other sorts, because you need to start with the original unsorted array. Here is a sample output: Initial Array The values array is: 88 49 69 19 03 54 57 83 42 48 92 72 78 10 08 13 46 29 73 9e 30 44 80 74 66 60 79 36 05 63 09 97 62 60 21 51 63 83 87 22 08 18 48 41 38 22 58 99 19 94 0 swaps. comparisons. SelectionSort The values array is: 03 05 08 08 09 10 13 18 19 19 21 22 22 29 30 36 38 41 42 44 46 48 48 49 51 54 57 58 60 60 62 63 63 66 69 72 73 74 78 79 80 83 83 87 88 90 92 94 97 99 49 swaps 1225 comparisons. BubbleSort The values array is: 03 05 08 08 09 10 13 18 19 19 21 22 22 29 30 36 38 41 42 44 46 48 48 49 51 54 57 58 60 60 62 63 63 66 69 72 73 74 78 79 80 83 83 87 88 90 92 94 97 99 621 swaps 1225 comparisons