java program

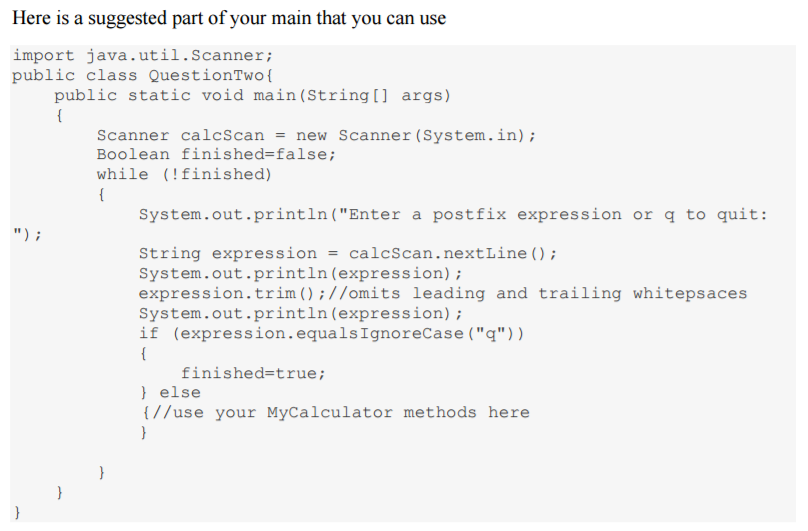
Question 1:

Stack.java

public interface Stack

{ boolean isEmpty(); boolean isFull(); T peek(); T pop(); void push(T t); void clear(); int size(); void reverse(); void display(); }

ArrayStack.java

public class ArrayStack implements Stack { private int capacity; private int size=0; private T[] stack; ArrayStack(int c) { capacity = c; stack = (T[])new Object[c]; } public T peek() { if(!isEmpty()) { T t = stack[size()-1]; return t; } else System.out.println("Stack is Empty(Underflow)!!!"); return null; } public T pop() { if(!isEmpty()) { T t = stack[size()-1]; size--; return t; } else System.out.println("Stack is Empty(Underflow)!!!"); return null; } public void push(T element) { if(!isFull()) { stack[size()]=element; size++; System.out.println("Element added!!!"); } else System.out.println("Stack is Full(Overflow)!!!"); } public void clear() { size=0; } public int size() { return this.size; } public boolean isEmpty() { return size()==0; } public boolean isFull() { return capacity=0;i--) { stk[i] = stack[size()-i-1]; } stack = stk; System.out.println("Reverse Completed!!!"); } else System.out.println("Stack is Empty(Underflow)!!!"); } public void display() { System.out.println(this); } public String toString() { String str=""; for(int i=0;i

ListStack.java

import java.util.List; import java.util.ArrayList; import java.util.Collections; public class ListStack implements Stack { private int capacity; private List stack = new ArrayList(); ListStack(int c) { capacity = c; } public T peek() { if(!isEmpty()) { T t = stack.get(size()-1); return t; } else System.out.println("Stack is Empty(Underflow)!!!"); return null; } public T pop() { if(!isEmpty()) { T t = stack.get(size()-1); stack.remove(size()-1); return t; } else System.out.println("Stack is Empty(Underflow)!!!"); return null; } public void push(T element) { if(!isFull()){ stack.add(element); System.out.println("Element added!!!"); } else System.out.println("Stack is Full(Overflow)!!!"); } public void clear() { stack.clear(); } public int size() { return stack.size(); } public boolean isEmpty() { return size()==0; } public boolean isFull() { return capacity You are to design a simple calculator using the ArrayStack implementation in Q1 to perform additions. subtractions, multiplications and divisions. The user may enter an arithmetic expression in infix using numbers (0 to 9), parentheses and arthmetic operations The first step to do so is to create a utility class MyCalculator that will have the following methods: Input of an expression and checking Balanced Parenthesis: public static Boolean isBalanced(String expression) This is a static method that will read a string representing an infix mathematical expression with parentheses from left to right and decide whether the brackets are balanced or not. To discover whether a string is balanced each character is read in turn. The character is categorized as an opening parenthesis, a closing parenthesis, or another type of character. Values of the third category are ignored for now. When a value of the first category is encountered, the corresponding close parenthesis is stored in the stack. For example, when a is read, the character is pushed on the stack. When a is encountered, the character pushed is "H". The topmost element of the stack is therefore the closing value we expect to see in a well balanced expression When a closing character is encountered, it is compared to the topmost item in the stack. If they match, the top of the stack is popped and execution continues with the next character. If they do not match an error is reported. An error is also reported if a closing character is read and the stack is empty. If the stack is empty when the end of the expression is reached then the expression is well balanced