Keep getting errors regarding inconsistent numbers of samples

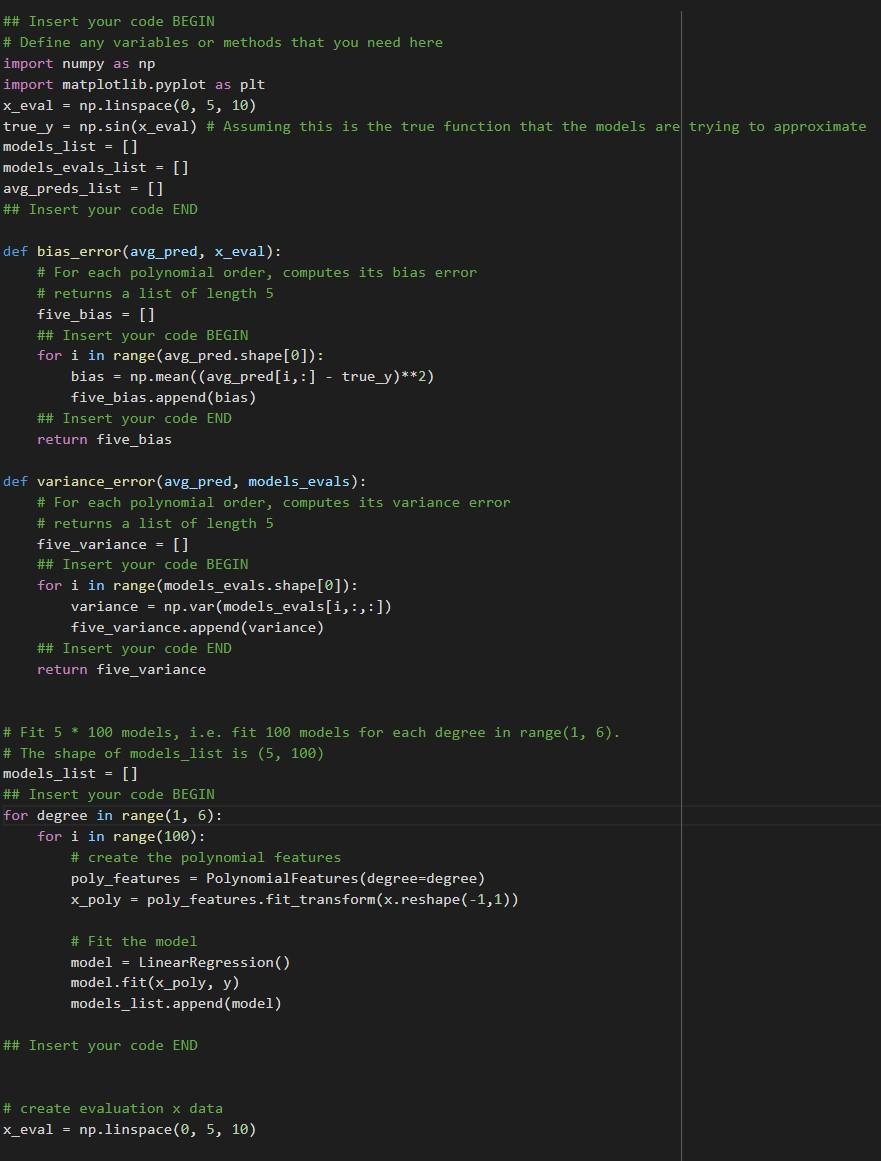
## Insert your code BEGIN

# Define any variables or methods that you need here

import numpy as np

import matplotlib.pyplot as plt

x_eval = np.linspace(0, 5, 10)

true_y = np.sin(x_eval) # Assuming this is the true function that the models are trying to approximate

models_list = []

models_evals_list = []

avg_preds_list = []

## Insert your code END

def bias_error(avg_pred, x_eval):

# For each polynomial order, computes its bias error

# returns a list of length 5

five_bias = []

## Insert your code BEGIN

for i in range(avg_pred.shape[0]):

bias = np.mean((avg_pred[i,:] - true_y)**2)

five_bias.append(bias)

## Insert your code END

return five_bias

def variance_error(avg_pred, models_evals):

# For each polynomial order, computes its variance error

# returns a list of length 5

five_variance = []

## Insert your code BEGIN

for i in range(models_evals.shape[0]):

variance = np.var(models_evals[i,:,:])

five_variance.append(variance)

## Insert your code END

return five_variance

# Fit 5 * 100 models, i.e. fit 100 models for each degree in range(1, 6).

# The shape of models_list is (5, 100)

models_list = []

## Insert your code BEGIN

for degree in range(1, 6):

for i in range(100):

# create the polynomial features

poly_features = PolynomialFeatures(degree=degree)

x_poly = poly_features.fit_transform(x.reshape(-1,1))

# Fit the model

model = LinearRegression()

model.fit(x_poly, y)

models_list.append(model)

## Insert your code END

# create evaluation x data

x_eval = np.linspace(0, 5, 10)

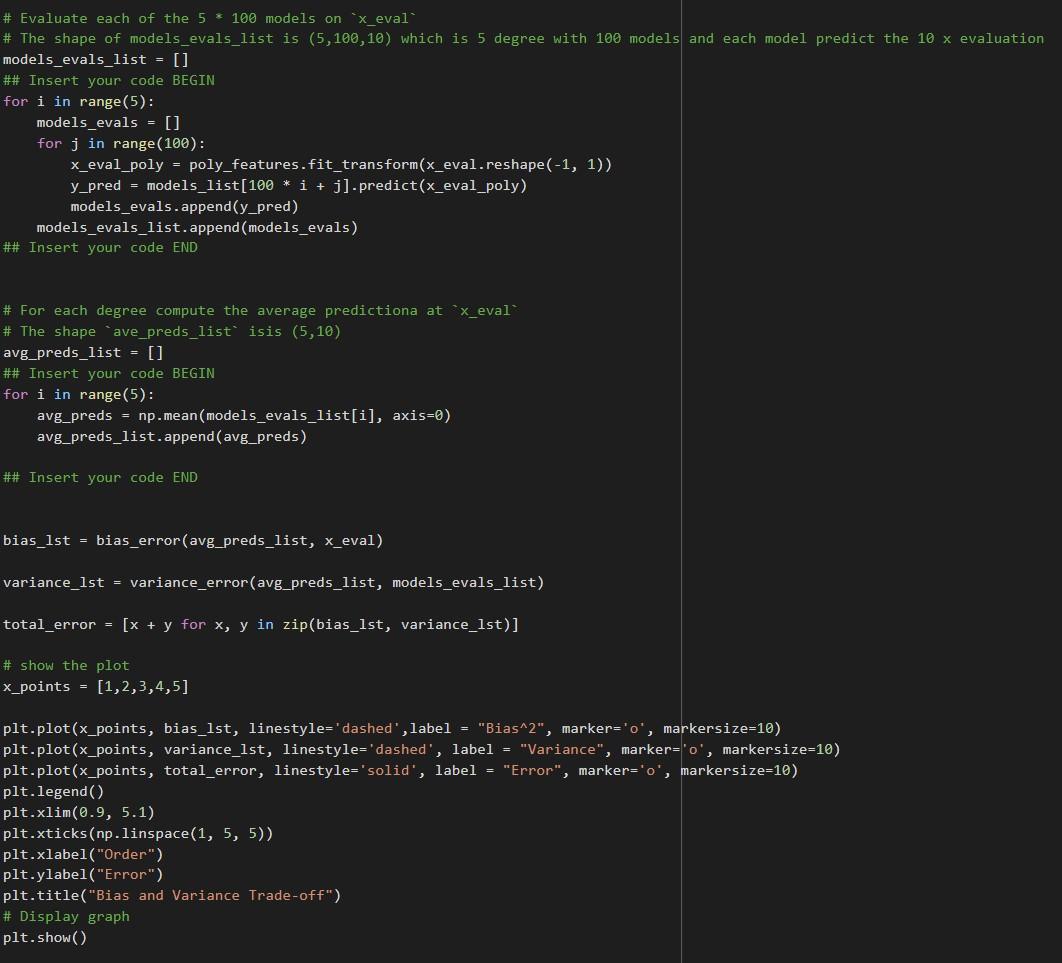
# Evaluate each of the 5 * 100 models on `x_eval`

# The shape of models_evals_list is (5,100,10) which is 5 degree with 100 models and each model predict the 10 x evaluation

models_evals_list = []

## Insert your code BEGIN

for i in range(5):

models_evals = []

for j in range(100):

x_eval_poly = poly_features.fit_transform(x_eval.reshape(-1, 1))

y_pred = models_list[100 * i + j].predict(x_eval_poly)

models_evals.append(y_pred)

models_evals_list.append(models_evals)

## Insert your code END

# For each degree compute the average predictiona at `x_eval`

# The shape `ave_preds_list` isis (5,10)

avg_preds_list = []

## Insert your code BEGIN

for i in range(5):

avg_preds = np.mean(models_evals_list[i], axis=0)

avg_preds_list.append(avg_preds)

## Insert your code END

bias_lst = bias_error(avg_preds_list, x_eval)

variance_lst = variance_error(avg_preds_list, models_evals_list)

total_error = [x + y for x, y in zip(bias_lst, variance_lst)]

# show the plot

x_points = [1,2,3,4,5]

plt.plot(x_points, bias_lst, linestyle='dashed',label = "Bias^2", marker='o', markersize=10)

plt.plot(x_points, variance_lst, linestyle='dashed', label = "Variance", marker='o', markersize=10)

plt.plot(x_points, total_error, linestyle='solid', label = "Error", marker='o', markersize=10)

plt.legend()

plt.xlim(0.9, 5.1)

plt.xticks(np.linspace(1, 5, 5))

plt.xlabel("Order")

plt.ylabel("Error")

plt.title("Bias and Variance Trade-off")

# Display graph