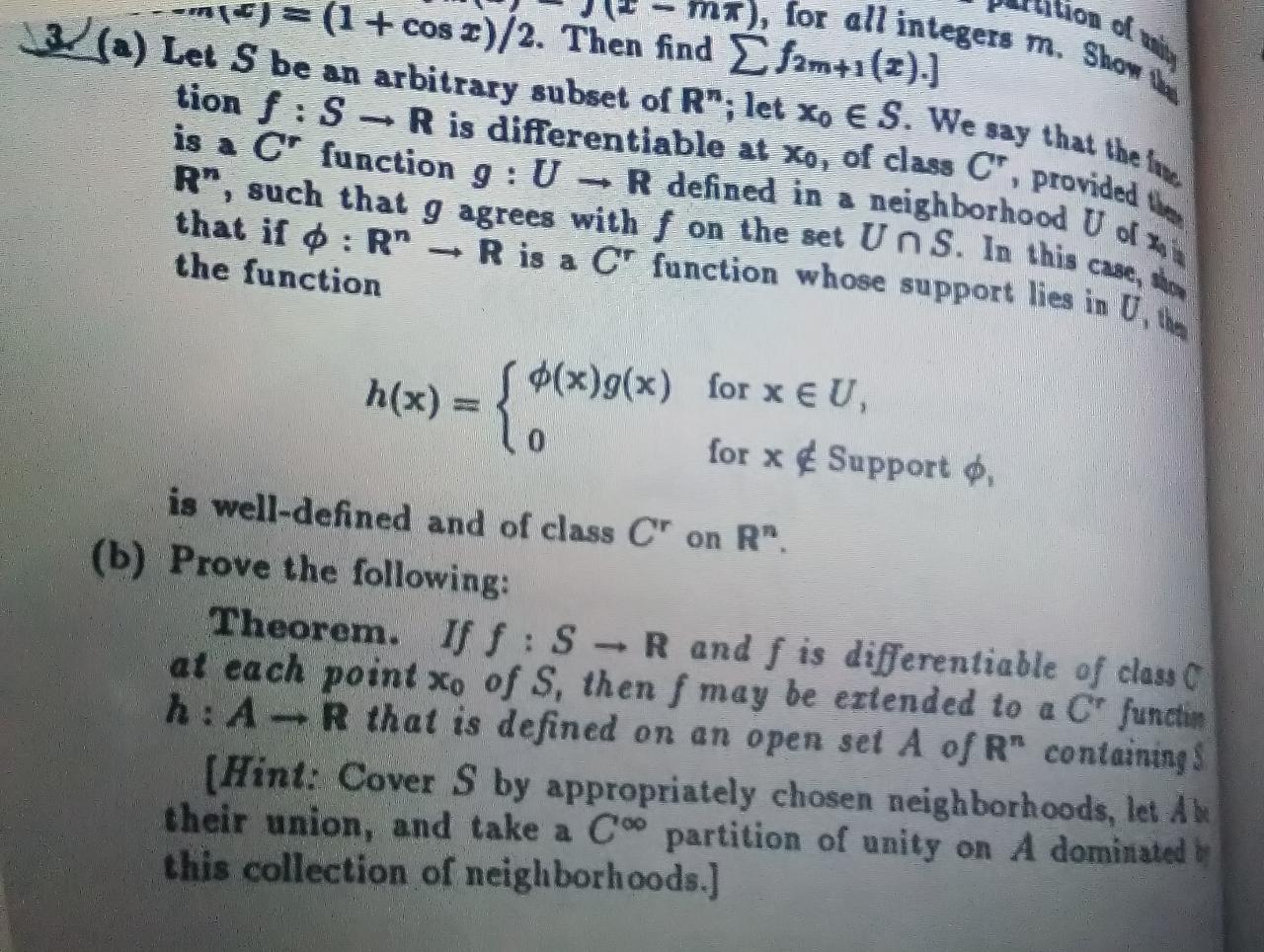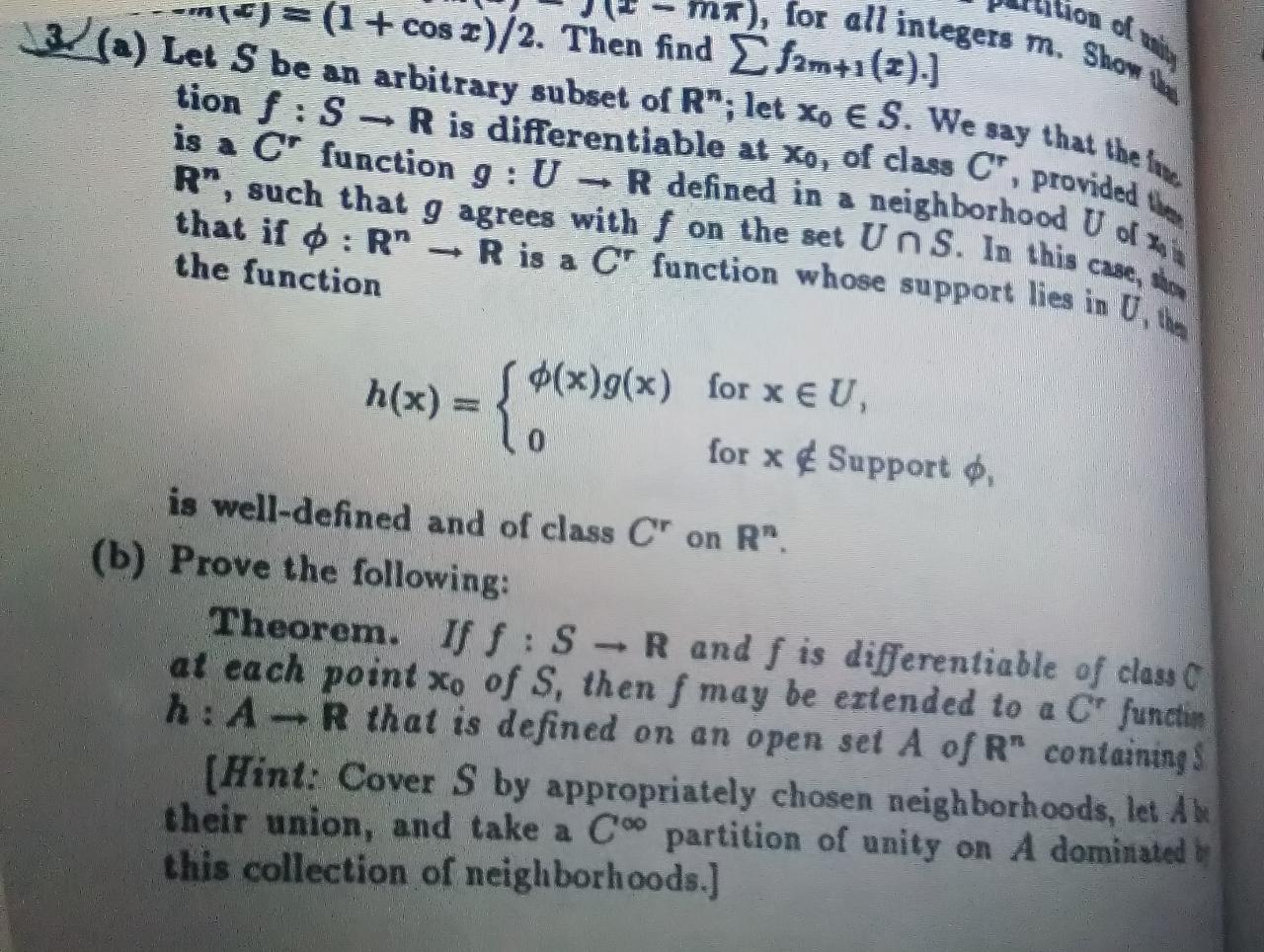
Kindly give only correct answers showing your steps

1. (a) Use the Intermediate Value Theorem to show that the equation - sin (x) + sin(x) =-1 has at least two distinct real solutions on (0, ce). Justify your answer. (b) Let ( fa)=2 be the sequence of functions defined by: 1 -nex, fu( x) = 0. 2 it xe [ 3. 1 ] (1) Find the pointwise limit of the sequence of functions (.),2 Does the sequence ( ,), , converge uniformly on [0. 1| to its pointwise limit? Justify your answers Let a. B E N. and f : 8 - R be the function defined by: B (sin (;))" cos (!). f( x) = For cr EN and B > 2, show that function / is differentiable on R. and give the value of f(x) for allre R. (1) For de N and B - 1, show that / is not differentiable at 0.(") Does the sequence (f,),-2 converge uniformly on [0, 1] to its pointwise limit? Justify your answers. (c) Let a, B E N, and f : R -+ IR be the function defined by; B (sin ()) " cos (!) . it x*#0 f (x ) = if x = 0. () For a E N and B 2 2, show that function / is differentiable on R, and give the value of f'(x) for all .x e R. (1) For a E N and B = 1, show that f is not differentiable at 0. Justify your answers. id) Let to E R. and f. g : R > R be real functions. Consider the function / : R R defined by where @ is the set of rational numbers. Show that if / and g are continuous functions at a and (to) - gian), then h is continuiton of ( mx), for all integers m. Show -m (*) = (1 + cos x)/2. Then find _ fam+1 (2).] 3(a) Let S be an arbitrary subset of R"; let Xo E S. We say that the fou. tion f : S - R is differentiable at xo, of class C", provided ( is a C" function g : U - R defined in a neighborhood U of 2. R", such that g agrees with f on the set Un S. In this case, that if o : R" - R is a C' function whose support lies in Up the function S $(x)g(x) for x E U, h(x) = for x @Support $, is well-defined and of class C' on R". (b) Prove the following: Theorem. If f : S - R and f is differentiable of class C at each point xo of S, then f may be extended to a C" functin h : A - R that is defined on an open set A of R" containing s [Hint: Cover S by appropriately chosen neighborhoods, let A their union, and take a Coo partition of unity on A dominated by this collection of neighborhoods.]Problem 4: Let f, g be functions which are both differentiable at a = c. Moreover, assume that f(c) = g(c) = 0 and g'(c) # 0. Prove that lim f(I) f'(c) reg(r) -g' (c) (Note that this is not L'Hospital's rule.) Problem 5: Let f be a real valued function on R. If for some number B > 1, If (z) - f(y)| ro, then f(r) zo