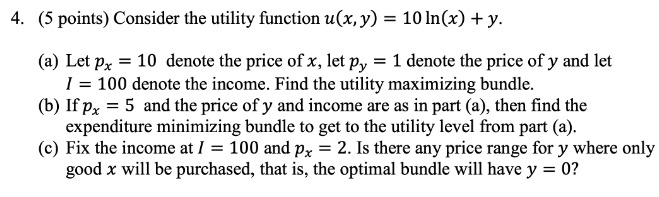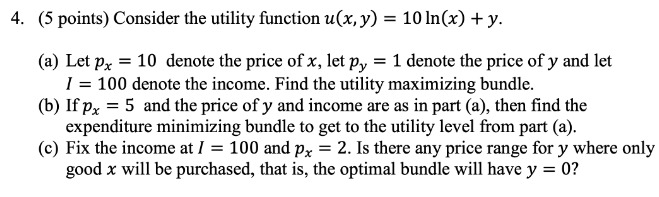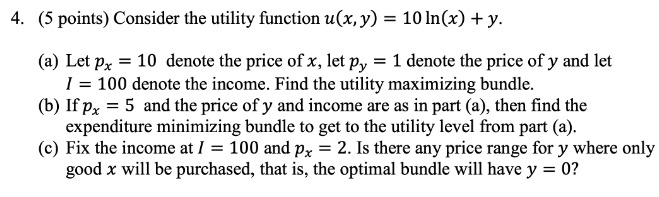



Kindly solve these for me
4. (5 points) Consider the utility function u(x, y) = 10 In(x) + y. (a) Let px = 10 denote the price of x, let py = 1 denote the price of y and let / = 100 denote the income. Find the utility maximizing bundle. (b) If px = 5 and the price of y and income are as in part (a), then find the expenditure minimizing bundle to get to the utility level from part (a). (c) Fix the income at / = 100 and p. = 2. Is there any price range for y where only good x will be purchased, that is, the optimal bundle will have y = 0?Problem 3: The market for product Q has many identical firms, each having the short-run total cost function: STC(q) = 400+5q+q?, where q is the firm's annual output. We also know that the market demand curve for Q is given by: Q =262.5 - 0.5P, where P is the market price. Each firm is currently earning zero economic profit. (a) Calculate numeric values for: E the market price, (ii) each firm's output, the number of firms in the market. (b) State the market level supply curve. (c) Draw the market and firm demand/supply graphs and show your results from parts (a) and (b).4. A firm produces computers with two factors of production: labor L and capital K. It's pro- duction function is 10 Suppose the factor prices are wy = 10 and wx - 100. (a) Graph the isoquants for y equal to 1,2, and 3. Does this technology show increasing constant, or decreasing returns to scale? Why? (b) Derive the conditional factor demands. (c) Derive the long run cast function C'(y) (d) If the firm wants to produce one computer, how many units of labor and how many units of capital should it use? How much will it cost? What if the firm wants to produce two computers of Derive the firm's long run average cost function AC(y) and long run marginal cost He tion 1/Cty Graph AC(v) and NIGIvy () Label the firm's long run supply curse on the graph.3. (36 points) Consider following production function: Y (K, L) = 200K1/2[1/2 a. Show that this production function exhibits constant returns to scale. b. Describe expansion path for output, given price of K and L as r and w respectively. Then fir input demand functions. C. Find wage elasticity of labor demand. d. Find average and marginal cost functions. e. Determine output elasticity of total cost. f. Confirm that firm produces at the minimum efficient scale. g. Calculate long-run cost function for the firm given r=w=100. What would be minimum cost for producing 100,000 units. What about 400,000? h. Suppose the firm can use 25 units capital in the short-run. Calculate short-run cost of the firm to produce 100,000 units given r=w=100. i. Suppose there is a change in technology and the new production function he in as Y = 200K1/2L