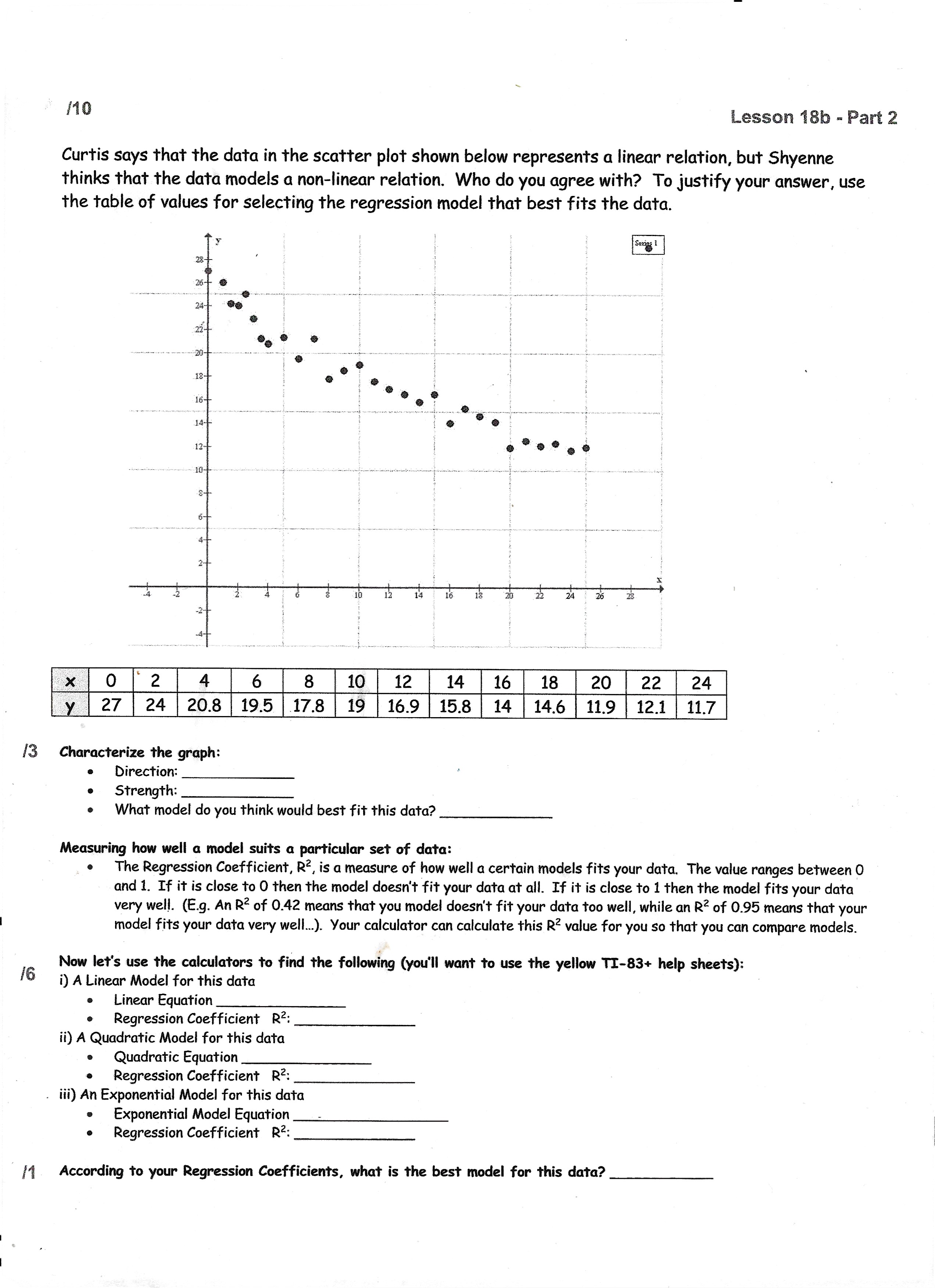
l3 l6 [1 \"0 Lesson 18b - Part 2 Curtis says that the data in the scatter plot shown below represents a linear relation, but Shyenne thinks that the data models a non-linear relation. Who do you agree with? To justify your answer, use the table of values for selecting the regression model that best fits the data. [Julian-"m Characterize the graph: - Direction: - Strength: . What model do you think would best fit this data? Measuring how well a model suits a particular set of data: 7 . The Regression Coefficient, R2. is a measure of how well a certain models fits your data. The value ranges between 0 and 1. If it is close to 0 then the model doesn't fit your data at all. If it is close to 1 then the model fits your data very well. (E.g. An R2 of 0.42 means that you model doesn't fit your data too well, while an R2 of 0.95 means that your model fits your data very well...) Your calculator can calculate this R2 value for you so that you can compare models. Now let's use the calculators to find the following (you'll want to use the yellow III-83+ help sheets): i) A Linear Model for this data . Linear Equation 0 Regression Coefficient R2: 7 ii) A Quadratic Model for this data . Quadratic Equation - Regression Coefficient R2: A iii) An Exponential Model for this data 0 Exponential Model Equation . Regression Coefficient R2: According to your Regression Coefficients, what is the best model for this data? Lesson 18b - Equation of Line of Best Fit 1. The table below shows Varsity Football Home Game Attendance. Game Attendance 1 222 2 285 3 399 641 529 VOUIA 952 1171 Create a properly labelled scatter plot using the data given in the table. (4 Marks) b. Draw a line of best fit. (2 Marks) c. What is the approximate slope of the line of best fit? (1 Mark) d. Using extrapolation, what would the approximate attendance be for game 9? Is this a safe assumption? Explain. (3 Marks) 2. The table below shows live bacteria count from a science experiment. Temperature 20 22 24 26 28 30 32 34 36 (C) Bacteria 2.1 4.3 5.2 6.1 6.7 7.6 10.3 8.2 14.1 (000s a. Graph the data in a scatter plot. (4 Marks) b. Determine the equation of the line of best fit. (2 Marks) c. Use your equation to predict the bacteria count when the temperature reaches 42 .C (2 Marks) d. What is the approximate degree, by using extrapolation, to find when the bacteria count when it reaches 18 000? (2 Marks)