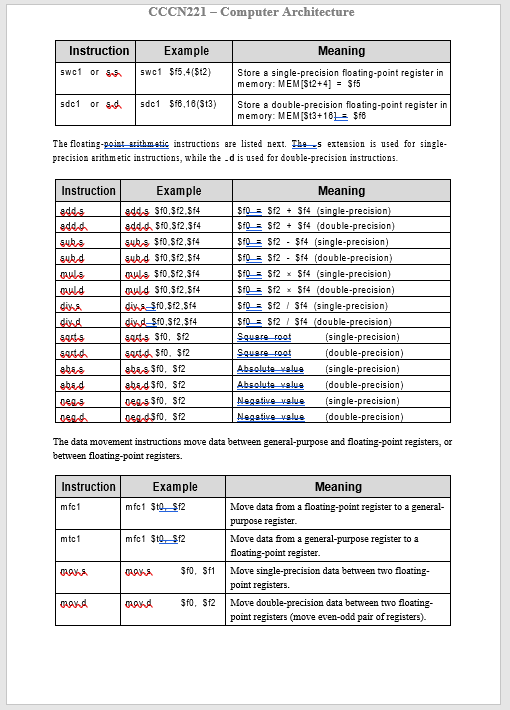
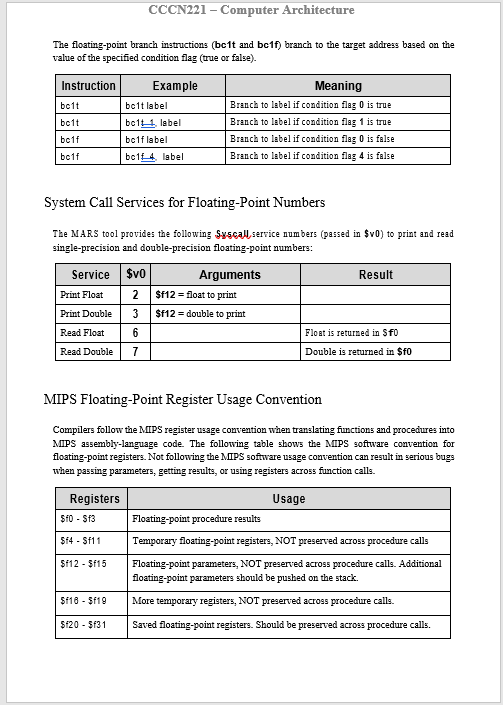
Lab 8-Floating points in MIPS In this lab, we will go through Floating-Point Number Repregentation (IEEE 754 Standard), have the basic understanding of MIPS Floating-Point Unit. Will write down programs using the MIPS FloatingPoint Instructions that will have the input and output as the floating point numbers. Floating-Point Number Representation Floating-point numbers bave been defined as follows \begin{tabular}{|l|l|l|} \hlineS & E= Exponent & F= Fraction \\ \hline \end{tabular} The Sign bit S is zero (positive) or one (negative). For aingle-precision the Exponent field E has 8 bits and for double-precision, 11 bits. The exponent field is biased. The Bias is 127 for single-precision and 1023 for double-precision The Fraction field F is 23 bits for single-precision and 52 bits for double-precision. Floating-point numbers are normalized (except when E is zero). There is an implicit 1 . (not stored) before the fraction F. Therefore, the value of a normalized floating-point number is: Value=(1.F)22EBlas Single Precision 754 Floating-Point Standard Figure 9.1: Floating-Point Representation MIPS Floating-Point Registers The floating-point unit (called coprocessor 1) has 32 floating-point registers. These registers are numbered as $f0,$f1,,$f31. Each register is 32 bits wide. Thus, each register can hold one gingle-precision floating-point number. How can we use these registers to store 64 -bit doubleprecision floating-point numbers? The answer is that the 32 single-precision registers are grouped into 16 double-precision registers. The double-precision number is stored in an even-odd pair of registers, but we only refer to the even-numbered register. For example, when we store a doubleprecision number in $f0, it is actually stored in registers $f0 and $f1. In addition, there are 8 condition flags, numbered from 0 to 7 . These condition flags are used by floating-point compare and branch instructions. These are ghown in Figure 9.2. Figure 9.2: QTSPIM Floating-Point Registers and Condition Flags MIPS Floating-Point Instructions The FPU supports geveral ingtructions including floating-point load and store, floating-point arithmetic operations, floating-point data movement instructions, convert, and branch instructions. We start this gection with the floating-point load and atore instructions. These instructions load into or atore a floating-point register. However, they use the same base-displacement addressing mode used with integer instructions. Notice that the base address register is an integer (not a floating-point) register. CCCN221 - Computer Architecture The floating-point-srithmetic instructions are listed next. Thg 5 extension is used for singleprecision arithmetic instructions, while the d is used for double-precision instructions. The data movement instructions move data between general-purpose and floating-point registers, or between floating-point registers. The convert instructions convert the format of data in floating-point registers. Three data formats are supported _s = single-precision float, d= double-precision, and .w= integer word. The floating-point compare instructions compare floating-point registers for equality, less than, and leas than or equal. The FP compare inatructions set the condition flags 0 to 7 to true (1) or false(0). The floating-point branch instructions (bc1t and bc1f) branch to the target address based on the value of the specified condition flag (true or false). System Call Services for Floating-Point Numbers The MARS tool provides the following s.xscallservice numbers (passed in $v0 ) to print and read gingle-precision and double-precision floating-point numbers: MIPS Floating-Point Register Usage Convention Compilers follow the MIPS register usage convention when translating functions and procedures into MIPS assembly-language code. The following table shows the MIPS software convention for floating-point registers. Not following the MIPS software usage convention can result in serious bugg when passing parameters, getting results, or using registers across function calls. Lab Tasks 1. Convert by hand the number 123456789 into its 32-bit single-precision binary representation, and Show your work for a full mark. 2. Convert by hand the floating-point number 11001010010011000001100000000000 (shown in binary) into its correaponding decimal value. Show your work for a full mark. 3. Trace the following program by hand to detemine the values of registers $f0 thru $f9. Notice that array1 and array2 have the same elements, but in a different order. Comment on the sums of array1 and array2 elements computed in registers $f4 and $f9, respectively. Now use the QTSPIM tool to trace the execution of the program and verify your results. What conclusion can be made from this exercise? -data arrayl: float 5.6e+20,5.6e+20,1.2 array2:-float 1.2,5.6e+20,5.6e+20 .text glgbl,main main: la 5 to, anawl lwcl $fop,0($t0) lwcl 5fl,4($t0) lwcl 5f,8($t0) addas $f3,$fl, \$fl adligi, 5f4,$f2,$f3 la 5 th araxt2 lwcl 5f5,0($t) lwcl 5 for. 4($t1) lwcl 5 ff. 8($t1) add,ai, $f8,$f5,$f6 adflek $fg,$fl,$f8 li 5v0,10 To terminate the program send main 4. Write an interactive program that inputs an integer sum and an integer count, computes, and displays the average = (float) sun / (float) count as a single-precision floating- point number. Hint: use the proper convert instruction to convert sum and count from integer word into single-precision float. 5. Write an interactive program that inputs the coefficient of a quadratic equation, computes, and displays the roots of the quadratic equation. All input, computation, and output ghould be done using double-precision floating-point instructions and registers. The program ghould handle the case of complex roots and displays the results properly. 6. Square Root Calculation: Newton's iterative method can be used to approximate the square root of a number x. Let the initial guess be 1 . Then each new guess can be computed as follows: guess =((x/ guess )+ guess )/2; Write a function called square spgtthat receives a double-precision parameter x, computes, and returns the approximated value of the square root of x. Write a loop that repeats 20 times and computes 20 guess values, then returns the final guess after 20 iterations. Use the MIPS floating-point register convention to pass the parameter x and to return the function result. All computation should be done using double-precision floating-point instructionsand registers. Compgre the resalt of the sqrtad instruction against the result of your squarescegt function. What is the error in absolute value