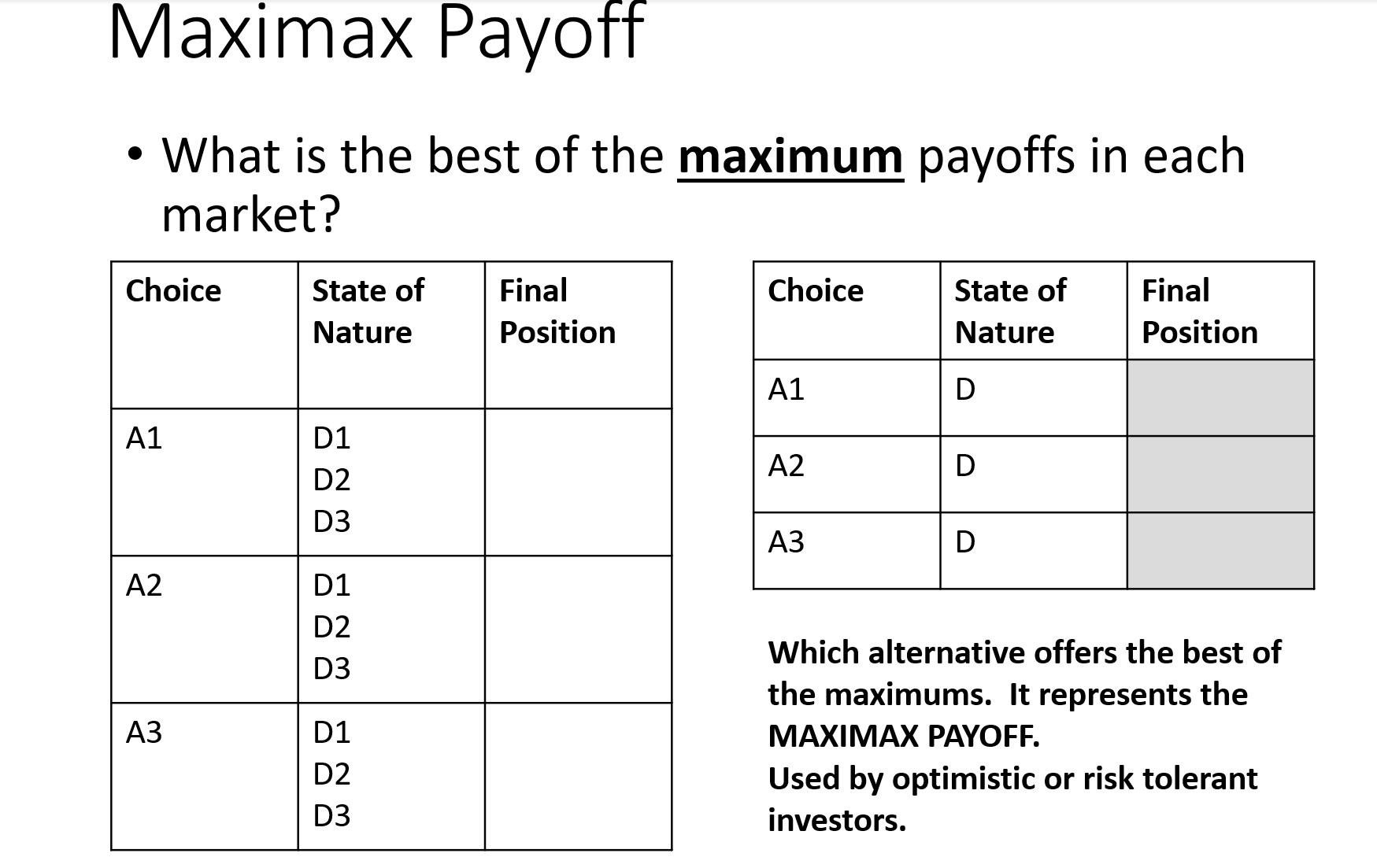
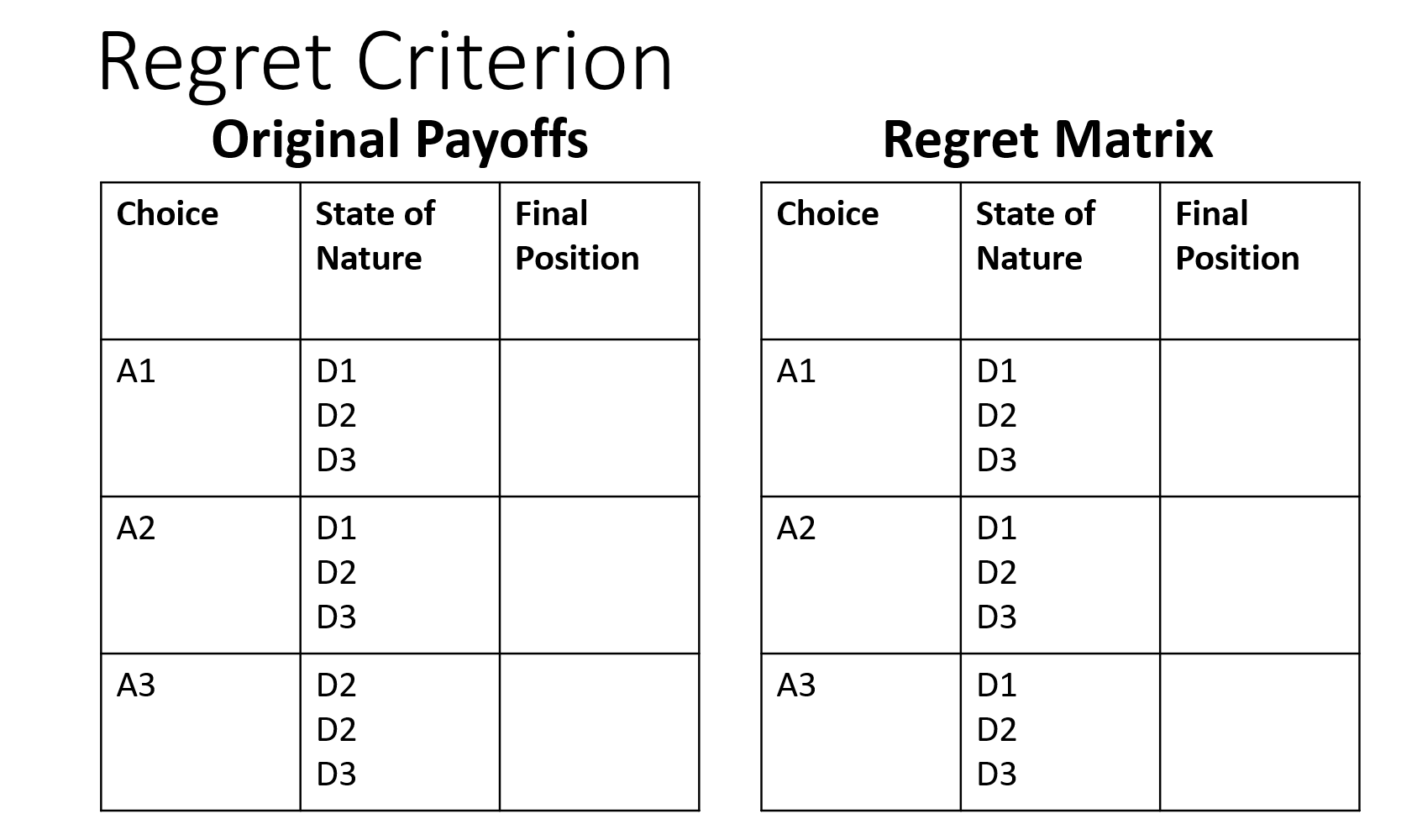
Laplace . Assume the probability of each state of nature (market condition) is equally likely. EV(A1) = (.3333 x FP1) + (.3333 x FP2) + (.3333 x FP3) EV(A2) = (.3333 x FP1) + (.3333 x FP2) + (.3333 x FP3) EV(A3) = (.3333 x FP1) + (.3333 x FP2) + (.3333 x FP3)IVIaXimin Payoff What is the best of the minimum payoffs in each market? Final Choice State of Final Position Nature Position A1 A2 Which alternative offers the best of the minimums? It represents the MAXIMIN PAYOFF. Used by pessimistic or risk averse investors. IVIaximax Payoff What is the best of the maximum payoffs in each Final Choice State of Final Position Nature Position market? Which alternative offers the best of the maximums. It represents the MAXIMAX PAYOFF. Used by optimistic or risk tolerant investors. Hurwicz Criterion Coefficient of Optimism Choice Maximum Minimum a = .6 (coefficient of optimism) Payoff Payoff (1 c1 ) = .4 (coefficient of pessimism) EV(A1) = (.6 x Max A1) + (.4 x Min A1) Which alternative yields the best EV(A2) = (.6x Max A2) + (.4x Min A2) return? \fSuppose you are the inventory manager of T-Shirts R Us. Your company is an online store that sells T-shirts and nothing else. Vou have to decide how many men's T-shirts to order for the summer season. You buy the T-shirts from an offshore manufacturer who imposes a condition on you; you have to order in batches of 100. If only 100 T-shirts are ordered, the cost is $10 per shirt, if 200 or more are ordered, the cost is $9 per shirt; and if 300 or more shirts are ordered the cost is $8.50 per shirt. The results of market survey provide you with information that the selling price will be $12 per shirt and that the possible sales levels are 100, 150, or 200 units; but you cannot assign any probability estimate to the alternative levels of demand or sales. If any T shirt remains unsold during summer, it can be disposed off at half the price ($6) in winter. The marketing manager also feels that there is a goodwill loss of $.50 for each T-shirt that consumers want to purchase from your shop but cannot because of stock-outs, It is not possible for you to wait for some time to study the nature (or determine the level) of demand, nor can you place more than one order. Thus, complete uncertainty prevails. As the inventory manager, you must decide how many T shirts to order in the face of uncertain demand. The three alternative strategies are to order 100 shirts (All, 200 shirts (A2) or 300 shirts (A3). The states of nature are three levels of demand: 100 (01). 150 (D2), Or 200 (D3). You are forced to make this decision in the face of uncertainty because you don't know what the demand level will be. Consequences are measures of the net benefit or payoff (reward) association with each ofthe levels of demand. The specific consequence or outcome depends not only on the decision (A1, A2, or A3) that is made but also on the event (D1, DZ, or D3) that occurs. There is a consequence or outcome associated with each combination of decision or action and event. These consequences are generally summarized in a payoff matrix. The Payoff Matrix: A payoff matrix is an essential tool of decision-making. It is a nice way of summarizing the interactions of various alternative action and events. Thus we can say that a payoff matrix provides the decision-maker with quantitative measures of the payoff for each possible consequence and for each alternative under consideration. Use the Powerpoint file named T-Shirts R Us to 1. Create the payoff matrix 2. Determine the best alternative order level (100, 200, or 300) using each of the following methods: a. Laplace b. Maximin c. Maximax cl. Hurwicz Criterion(ot= .6) e. Regret Criterion i. Complete the Regret Criterion Matrix ii. Answer the two questions on slide #10. Uncertainty (no probabilities associated with the market conditions) Payoff Matrix Choice States of Final 1. There are 3 alternatives: (Alter- Nature Position A1 Order 100 shirts at a cost of $10 each A2 Order 200 shirts at a cost of $9 each natives) (Events) (FP) A3 Order 300 shirts at a cost of $8.50 each 2. There are 3 states of nature or events: Order 100 D1 100 D1 Demand Level 1 you sell 100 shirts A1 D2 150 D2 Demand Level 2 you sell 150 shirts Cost $10 D3 200 D3 Demand Level 3 you sell 200 shirts Each shirt sells for $12 regardless of demand level. Order 200 D1 100 3. If you have stock-outs meaning your demand is A2 D2 150 higher than your order level, there is a loss of goodwill that cost $.50 per shirt. Cost $9 D3 200 4. At the end of the season, you can sell any unsold Order 300 D1 100 merchandise to a liquidator for $6 per shirt. A3 D2 150 5. Calculate the final position for each alternative at Cost $8.50 D3 200 each demand level