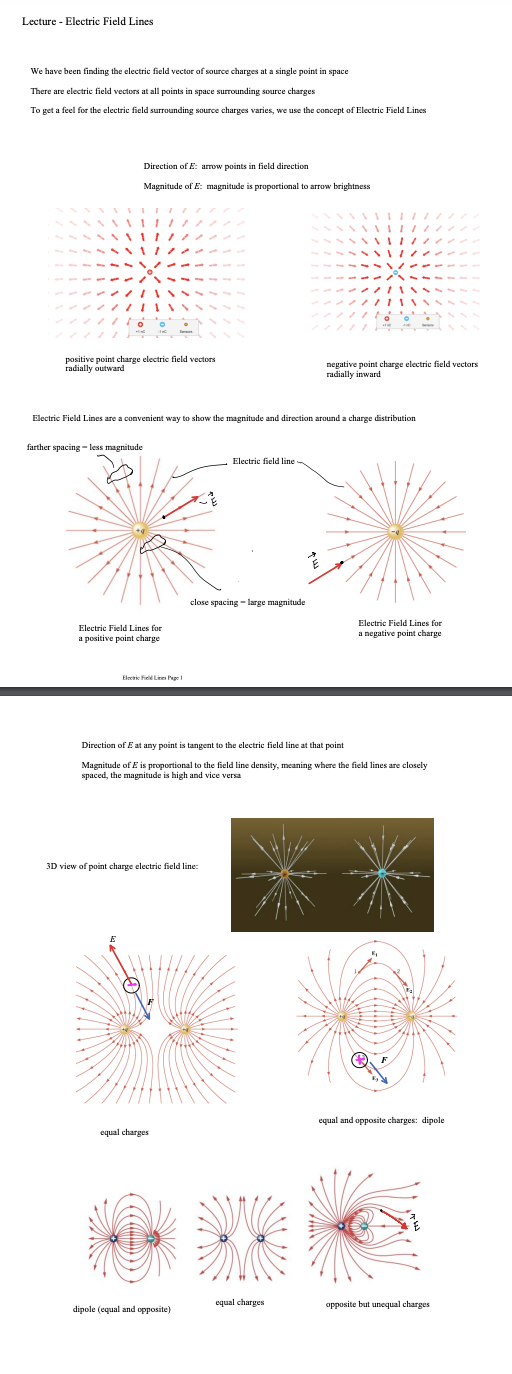
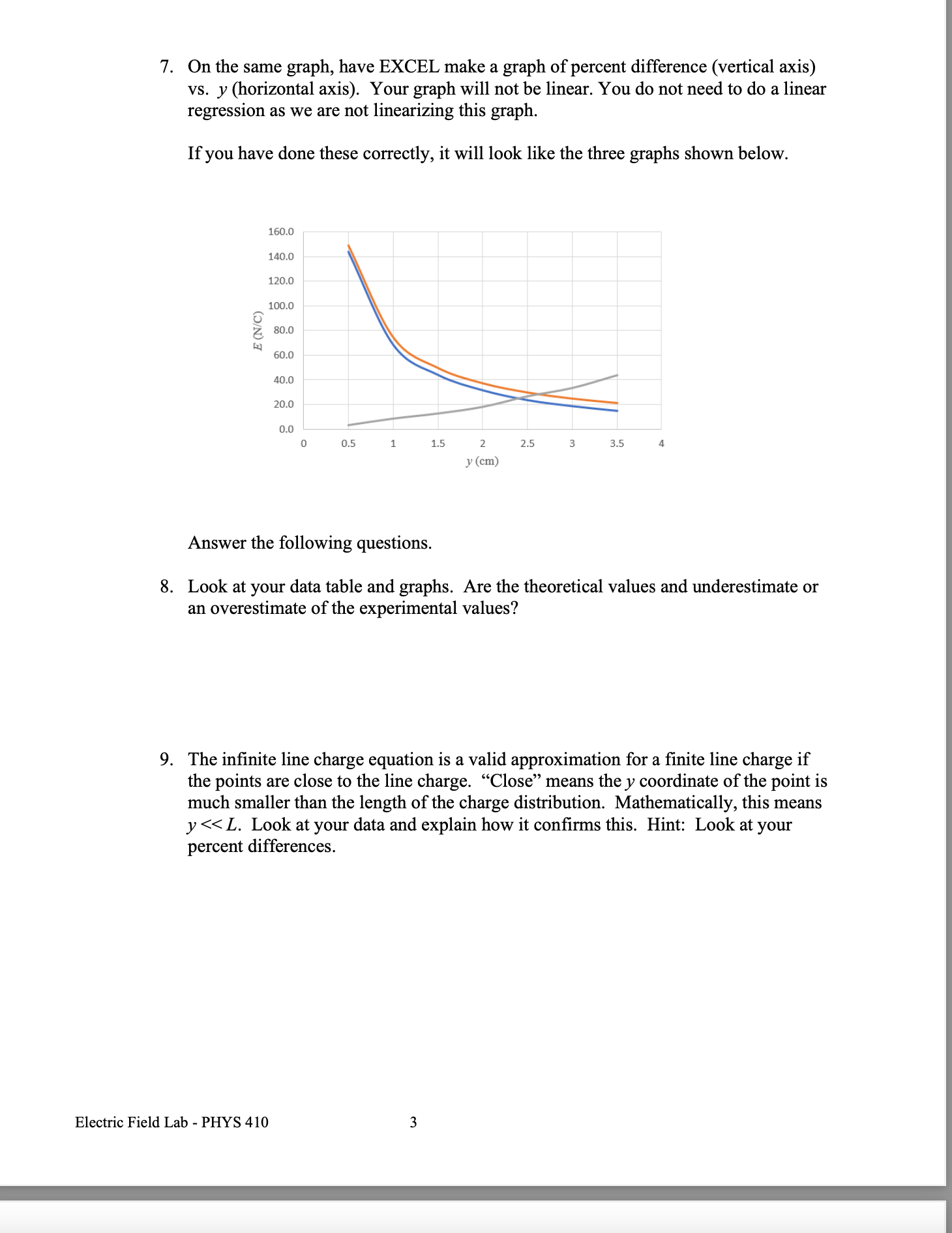
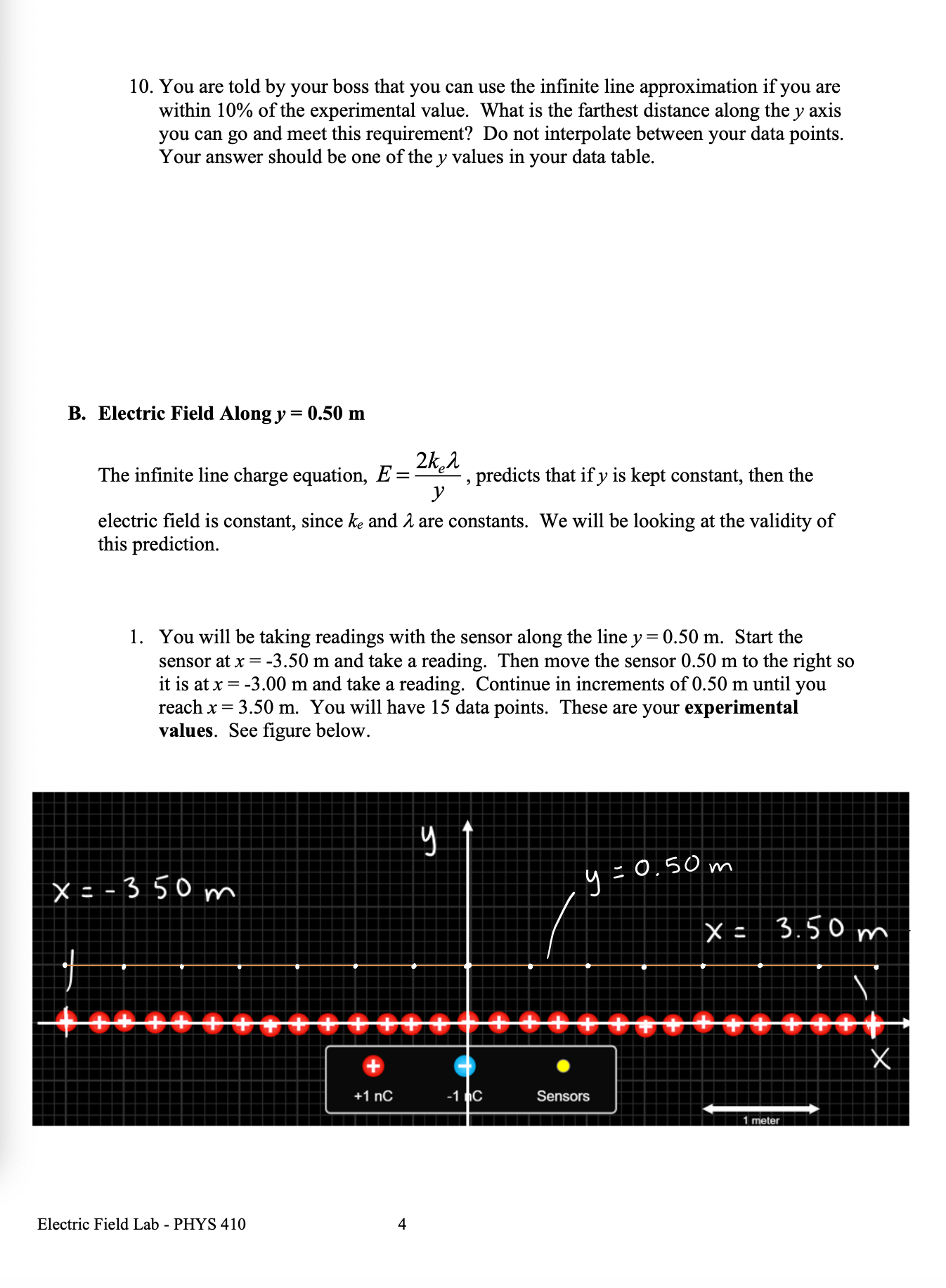
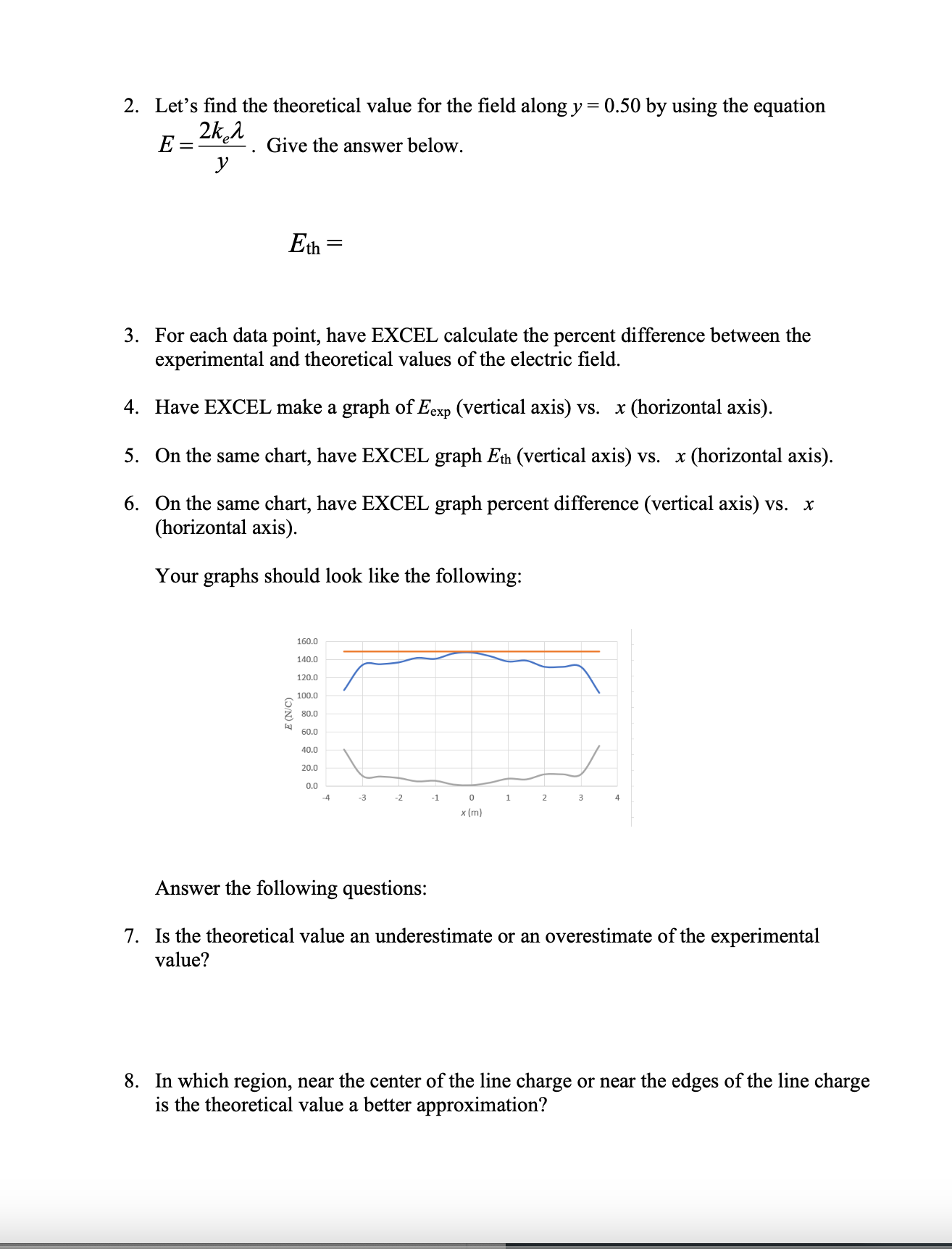
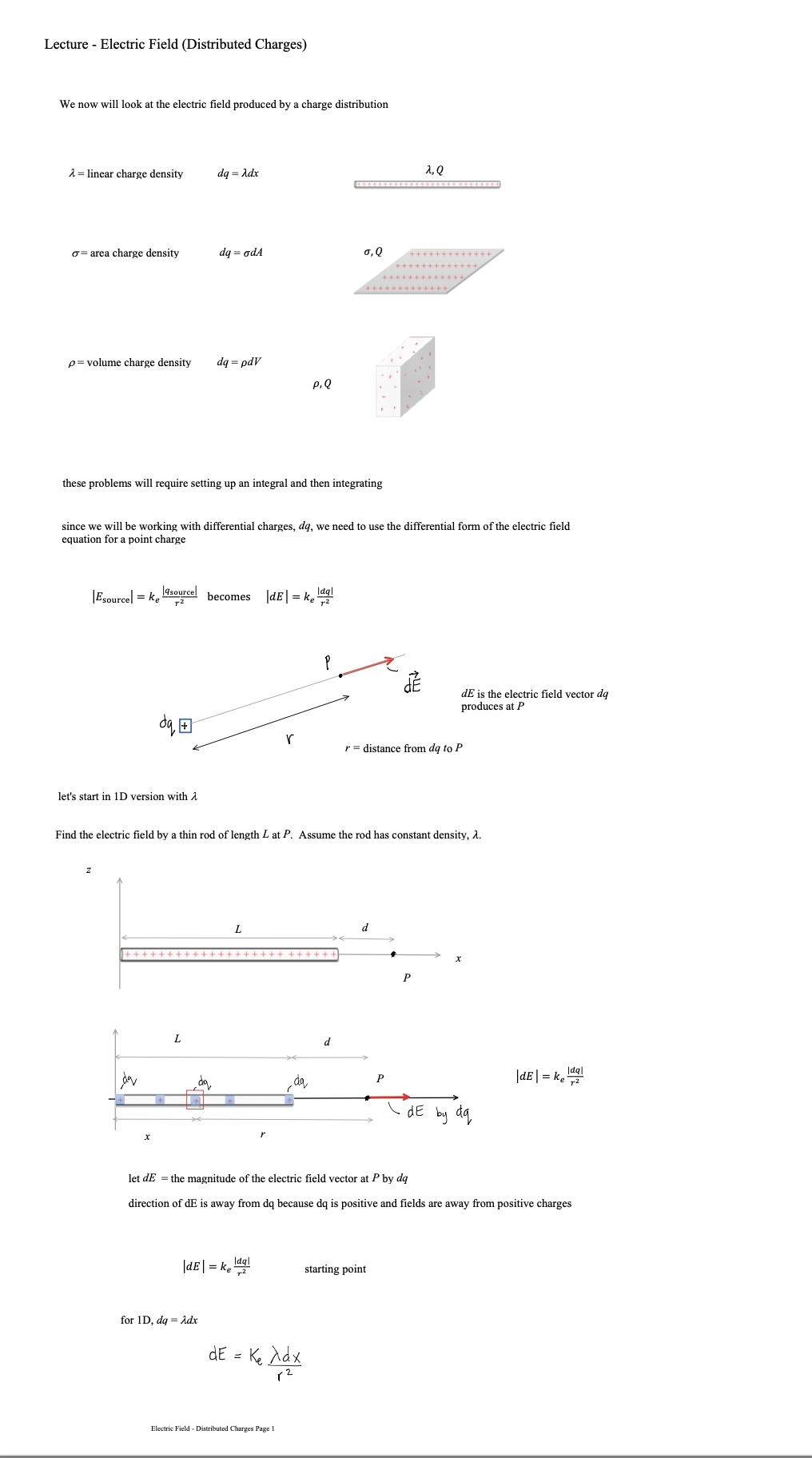
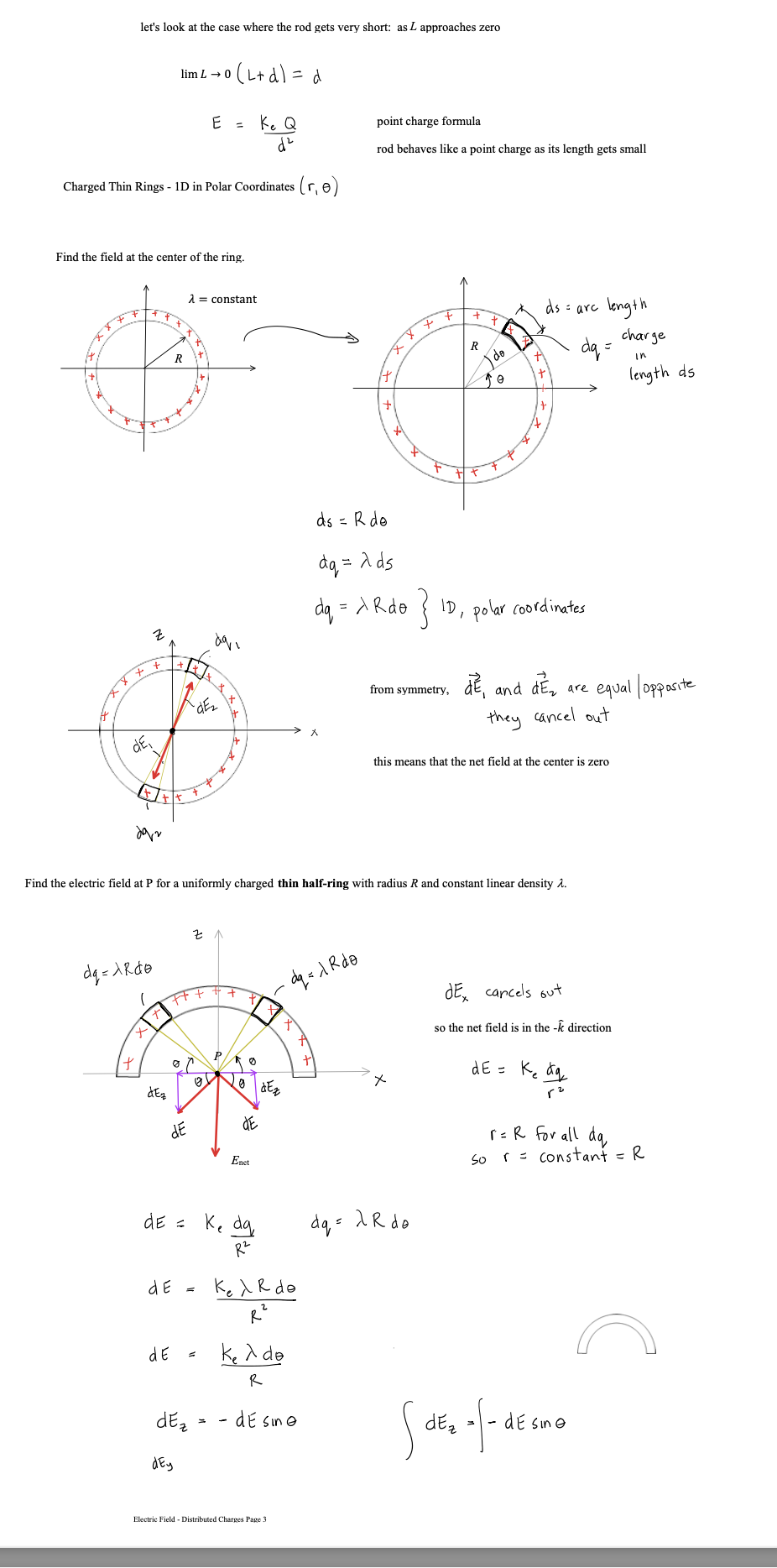
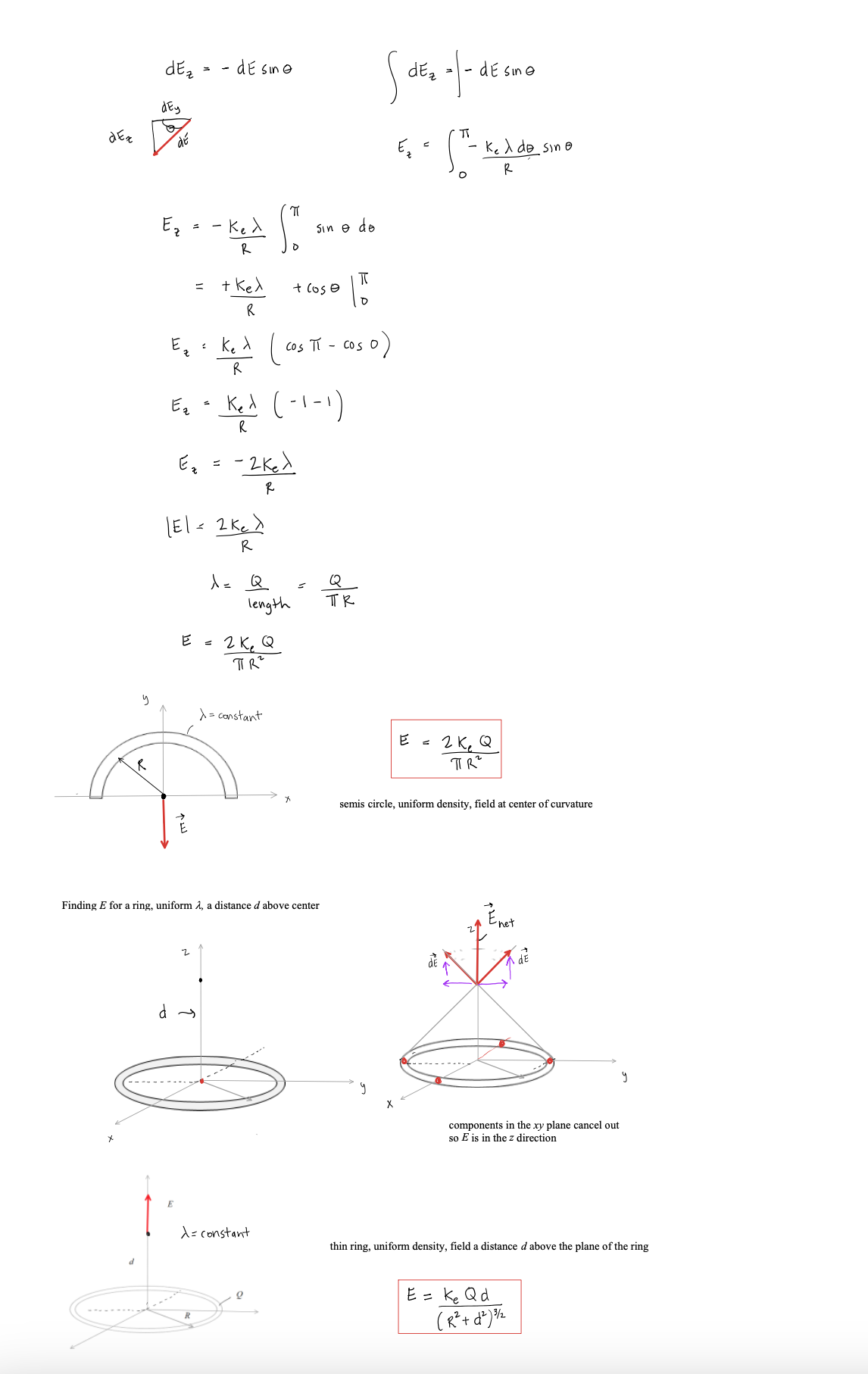
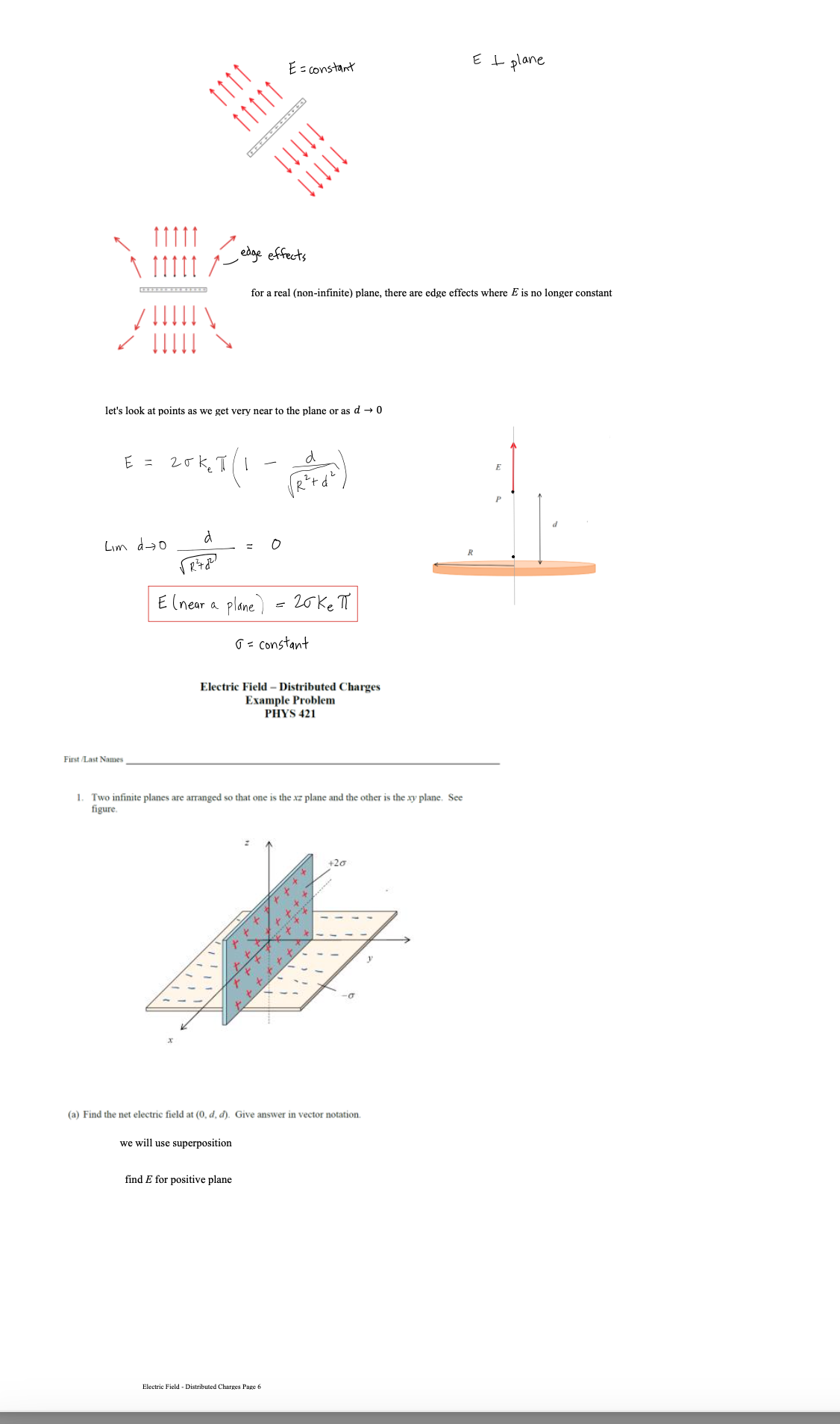
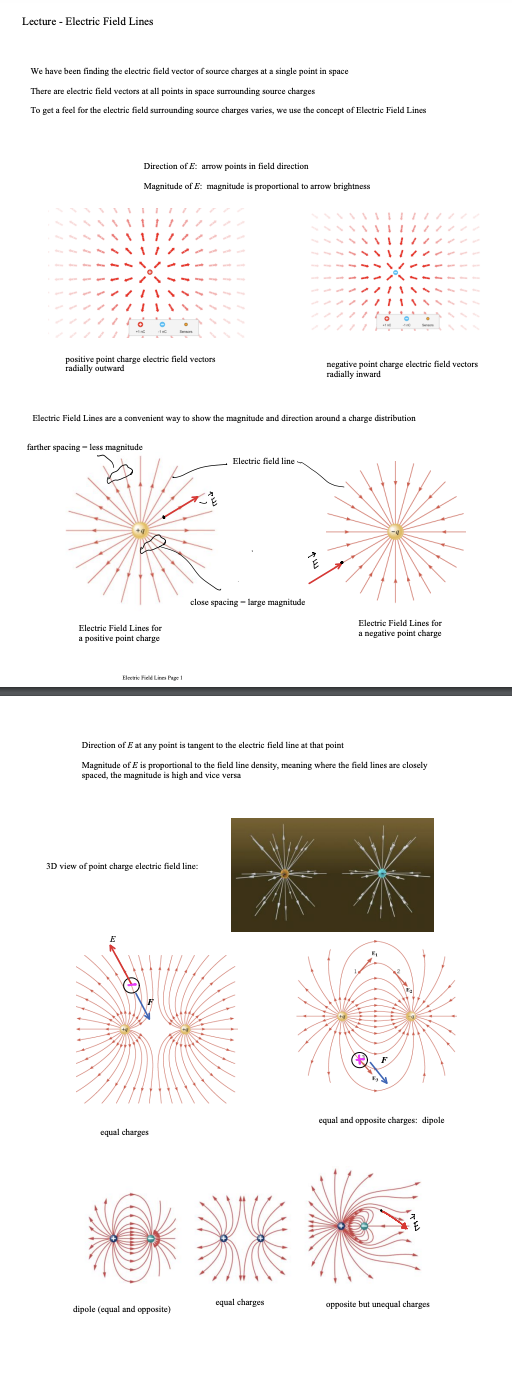
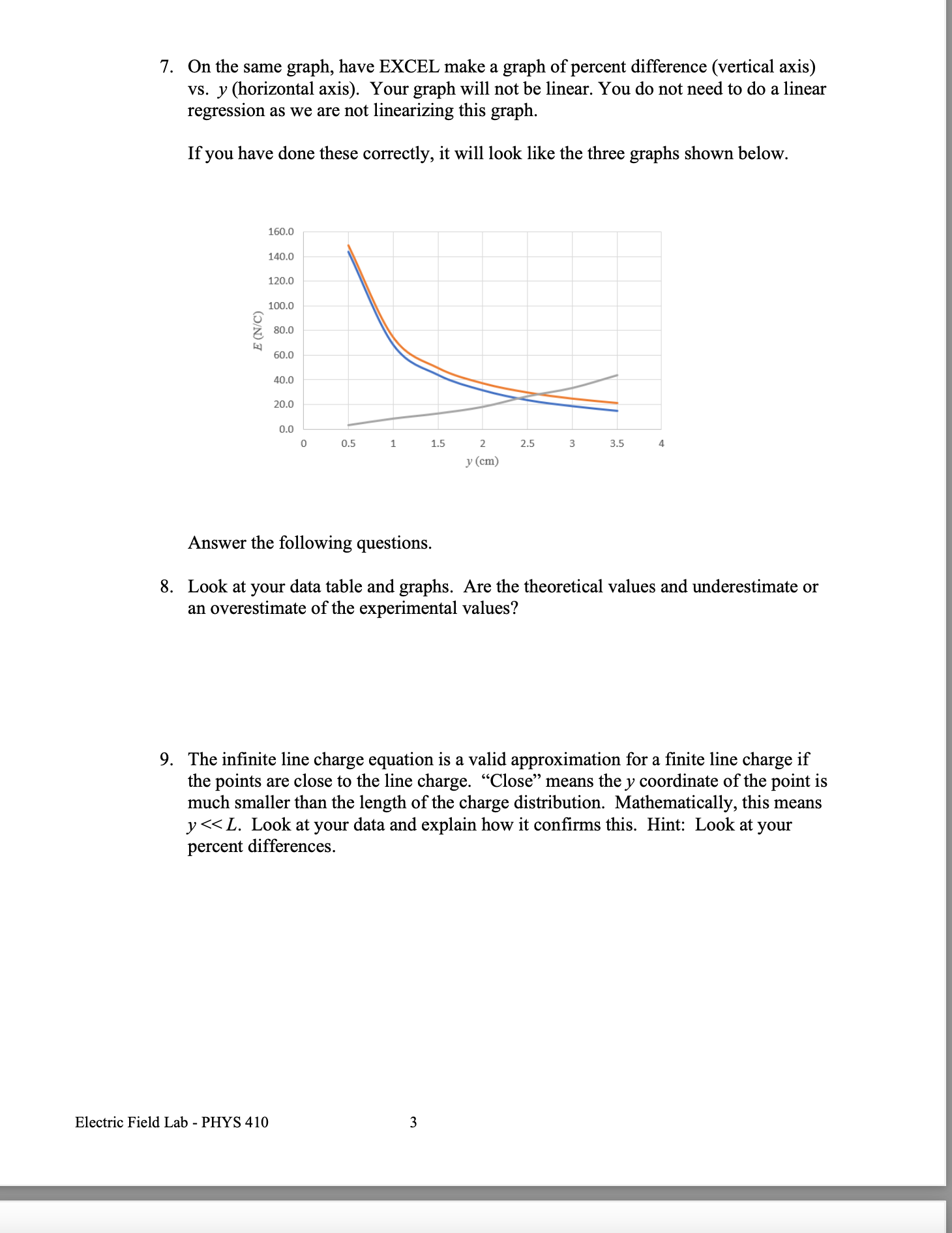
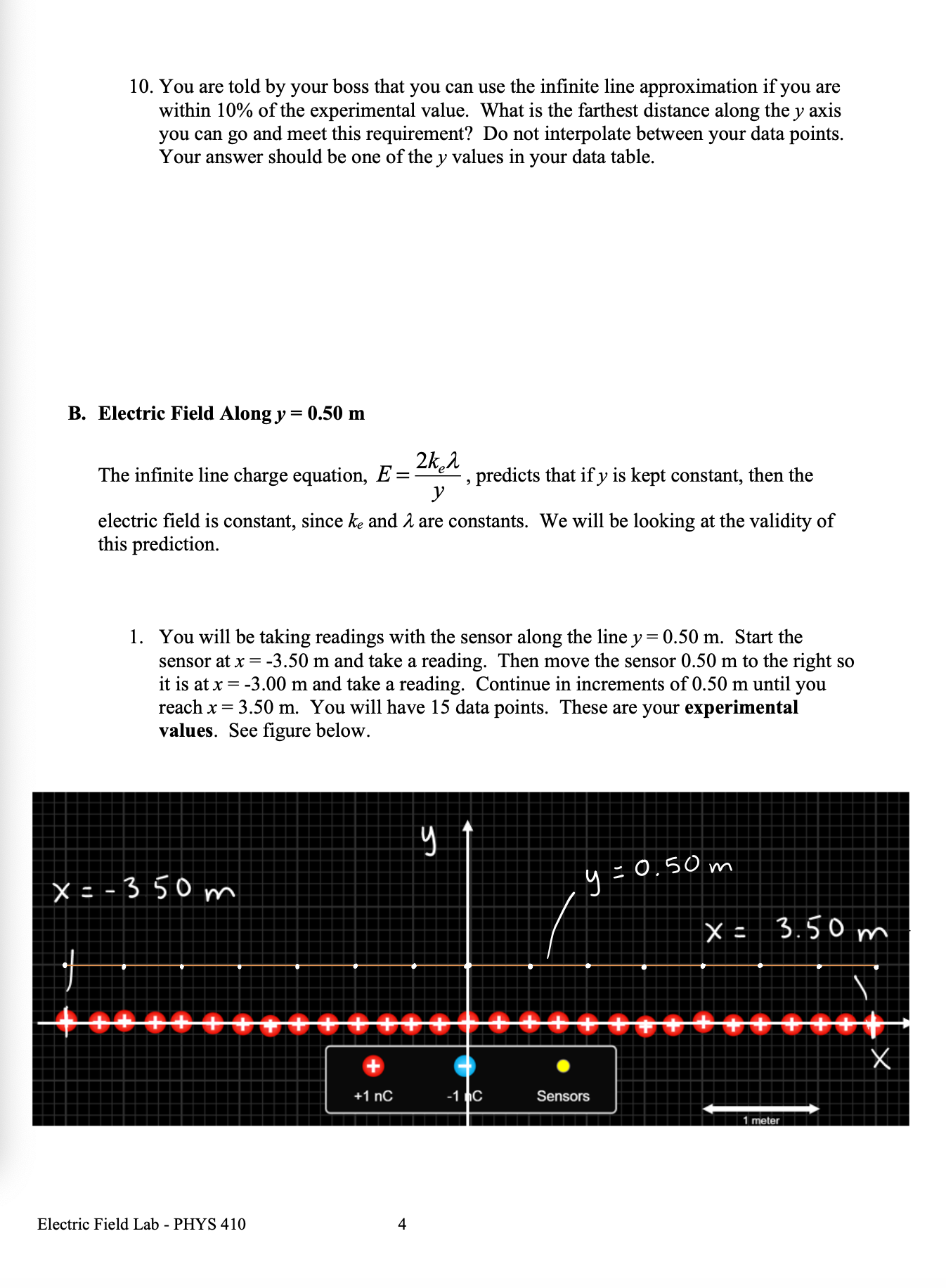
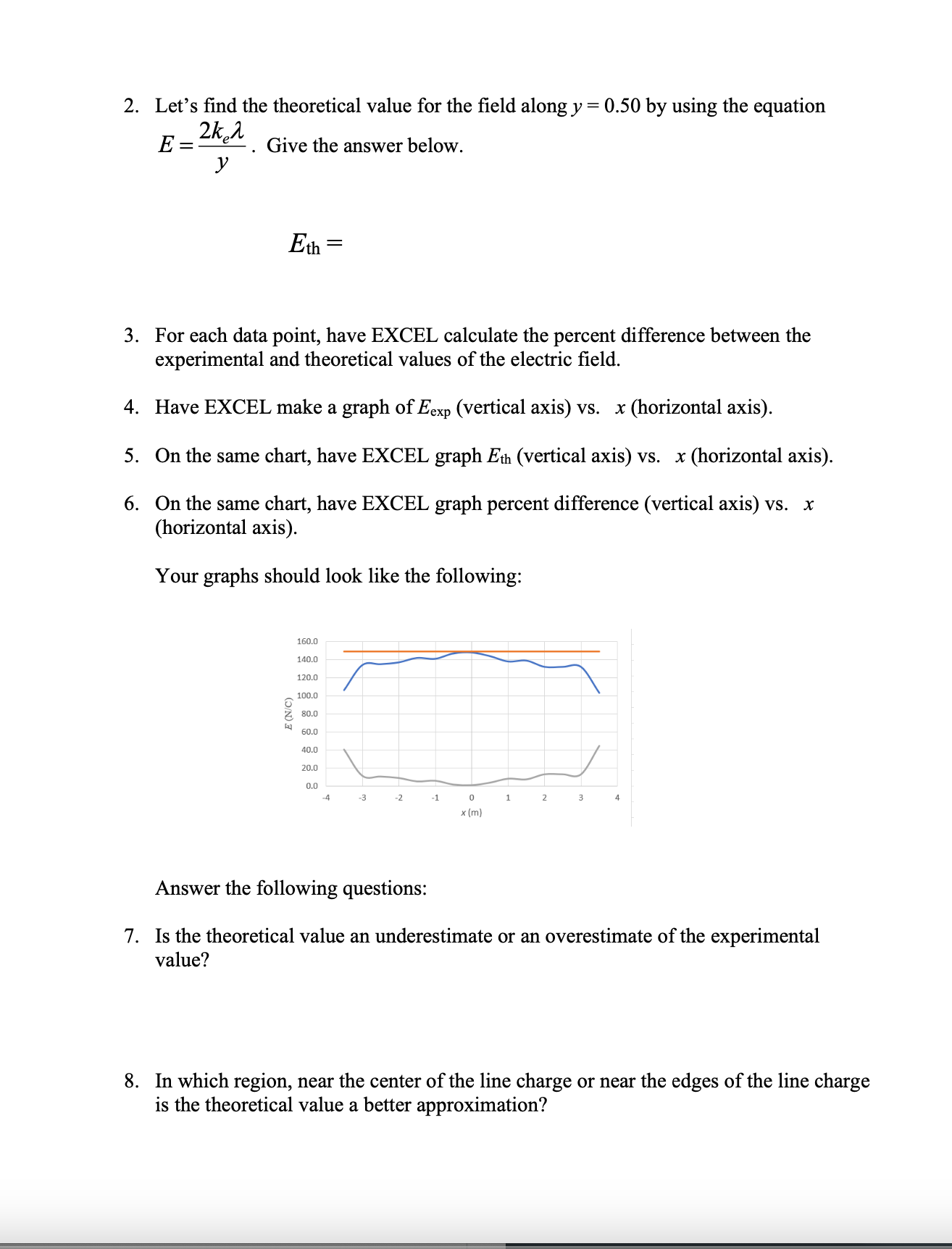
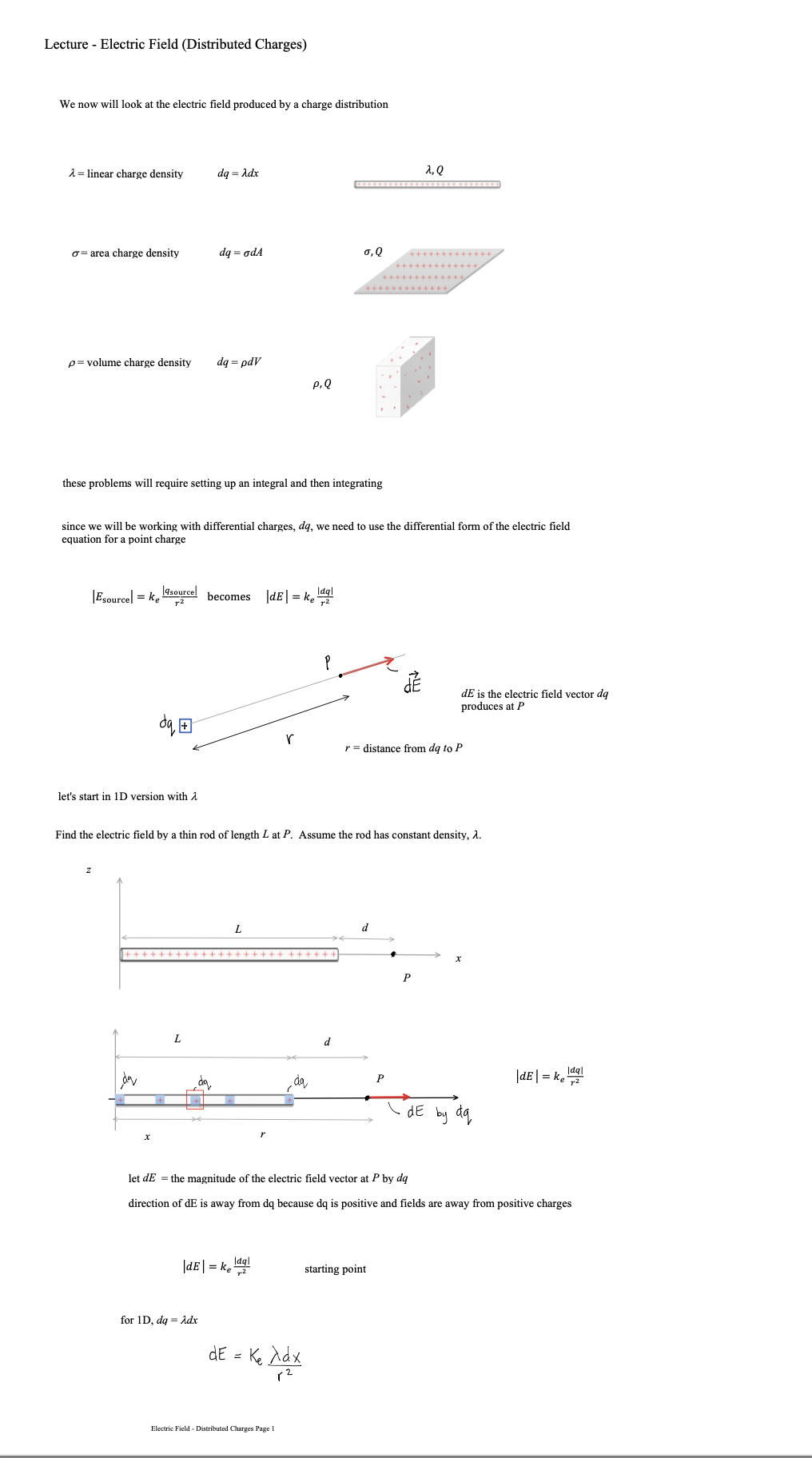
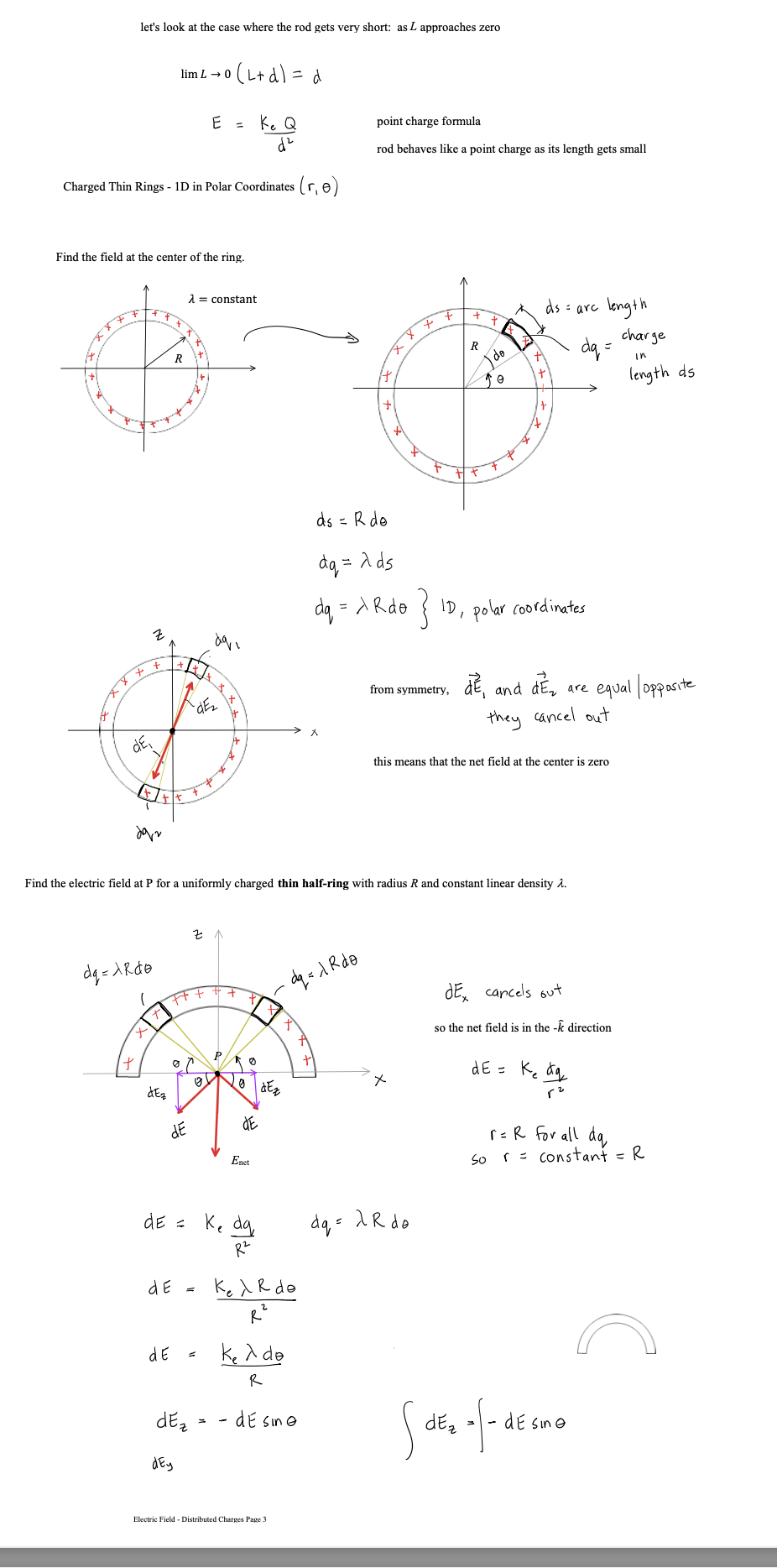
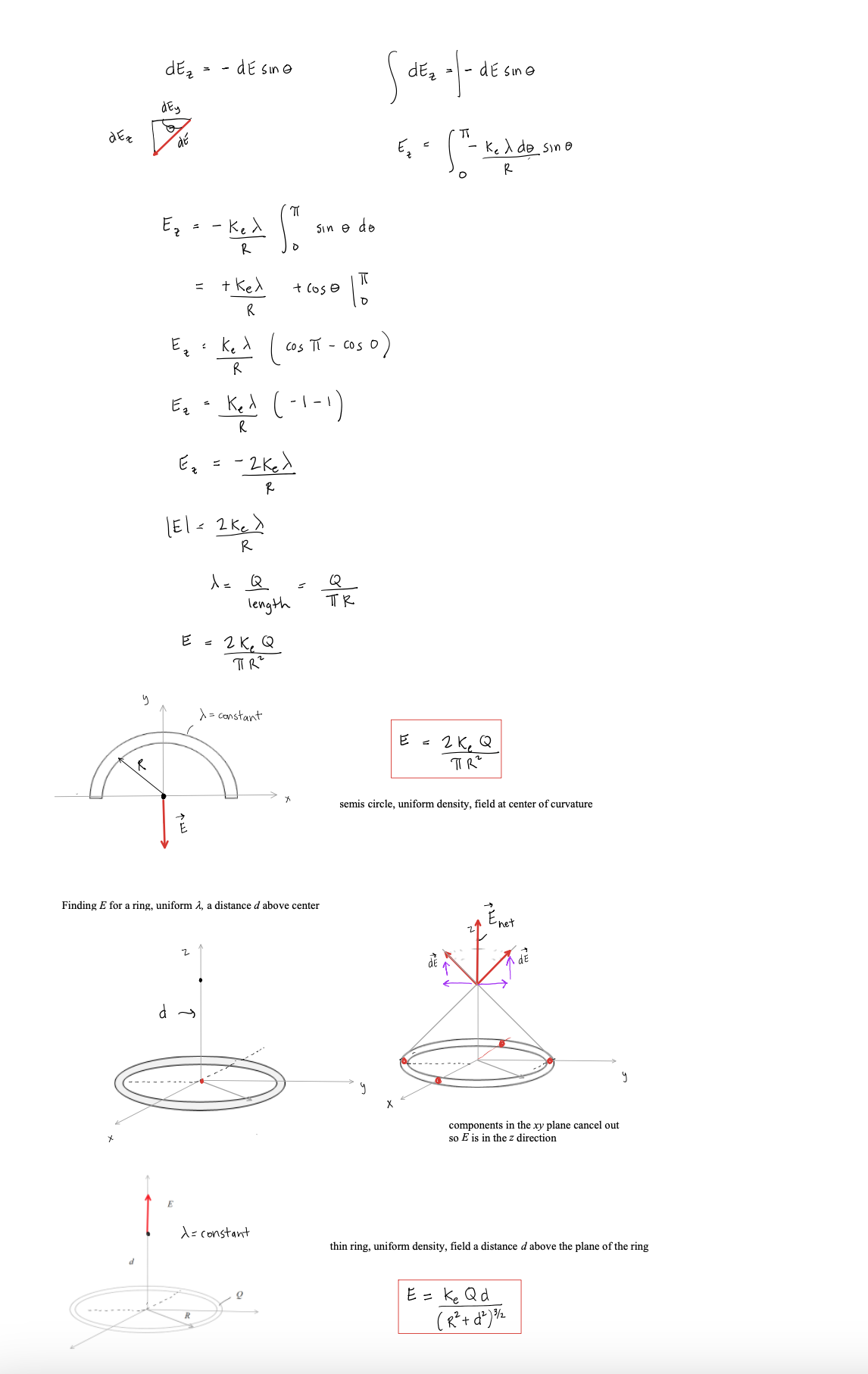
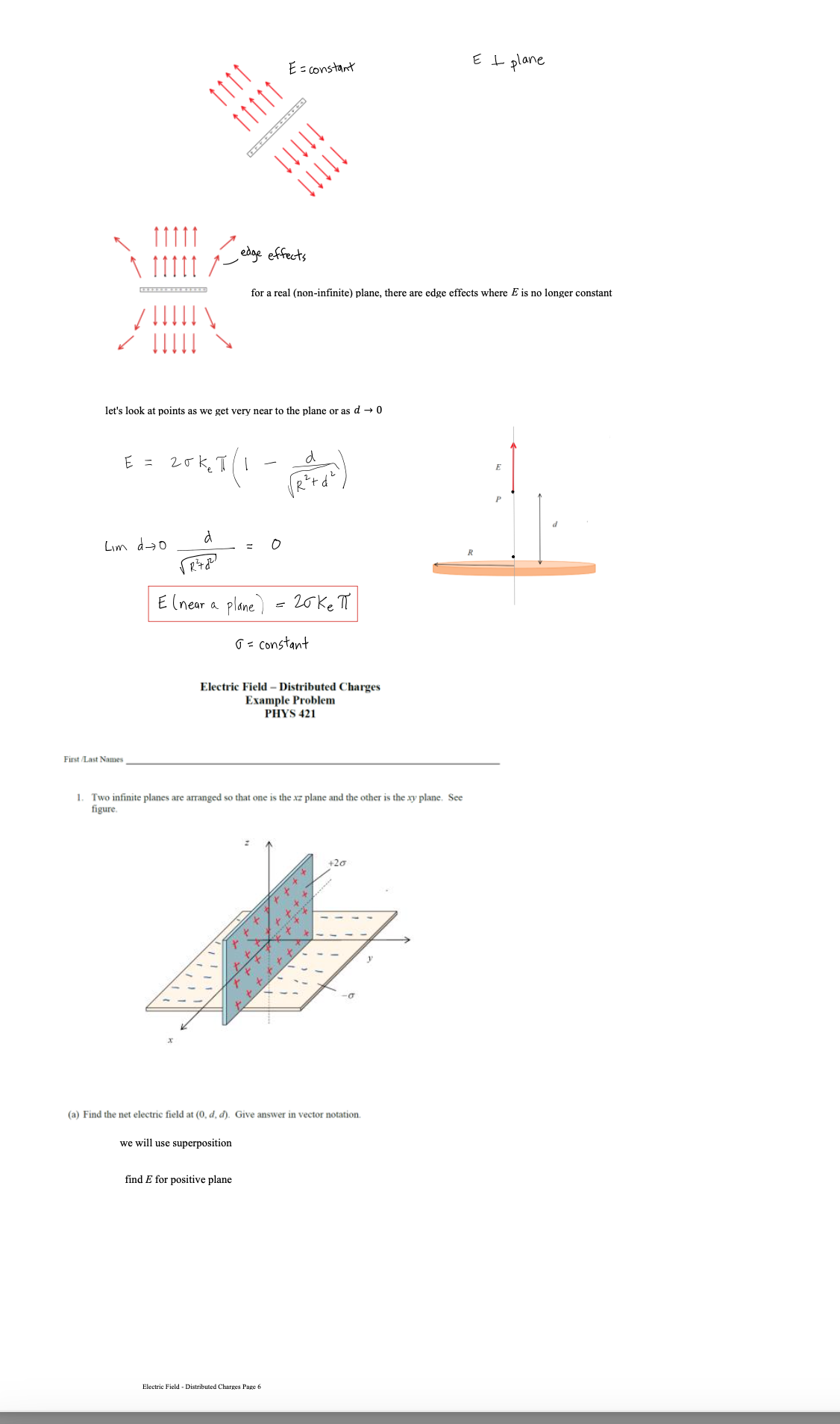
Lecture - Electric Field Lines We have been finding the electric field vector of source charges at a single point in space There are electric field vectors at all points in space surrounding source charges To get a feel for the electric field surrounding source charges varies, we use the concept of Electric Field Lines Direction of E: arrow points in field direction Magnitude of 2: magnitude is proportional to arrow brightness positive point charge electric field vectors radially outward negative point charge electric field vectors radially inward Electric Field Lines are a convenient way to show the magnitude and direction around a charge distribution farther spacing - less magnitude Electric field line close spacing = large magnitude Electric Field Lines for Electric Field Lines for a positive point charge a negative point charge Electric Field Lines Page 1 Direction of E at any point is tangent to the electric field line at that point Magnitude of & is proportional to the field line density, meaning where the field lines are closely spaced, the magnitude is high and vice versa 3D view of point charge electric field line: equal and opposite charges: dipole equal charges equal charges dipole (equal and opposite) opposite but unequal chargesThin Rod Infinite Plane - E is constant everywhere for a constant E, the electric field lines are straight, parallel and equally spaced in many cases, we are note concerned about the source that produces, just the effect the field has on the system Electric Field Lines Pape } no source shown just its field you CO say a system charge is placed in this field E since it is negative. the force it feels from the field is opposite to the field direction conductor placed in a uniform field what happens to this conductor? conductors have conduction electrons which are free to move the field will apply a force on the conduction electrons the force on electrons is to the left and the conductor becomes polarized what if you placed an insulator in the field?PHYS 421 Electric Field Lab - Distributed Charges Lab Group Members: This lab will use the phet simulation "Charges and Fields": https://phet.colorado.edu/sims/html/charges-and-fields/latest/charges-and-fields_en.html We will be looking at a finite, uniform line charge and investigating when it can be modeled as an infinite uniform line charge. Experiment A. Electric Field Along y Axis 1. Go to the simulation and check "Values" and "Grid". Note the distance scale at the bottom. Place twenty-nine +1 nC point charges along the axis, evenly distributed over a length of 7.00 m. The point charges will start at x = -3.50 m and end at x = 3,50 m. Place the charges as far down as possible. See figure below. X = - 350 m X = 3.50 m 1000004 0000 0 + X +1 nC Sensors 1 meter 2. Use the sensor to measure the electric field along the y-axis for values of y = 0.50 m, 1.00 m, 1.50 m, 2.00 m, 2.5 m 3.00 m, and 3.50 m. Record your results in an EXCEL table. These are your experimental values. Record your electric field values in units of N/C, not V/m. It is also best to use m, not cm for your y values. Electric Field Lab - PHYS 4107. On the same graph, have EXCEL make a graph of percent difference (vertical axis) vs. y (horizontal axis). Your graph will not be linear. You do not need to do a linear regression as we are not linearizing this graph. If you have done these correctly, it will look like the three graphs shown below. 160.0 140.0 120.0 100.0 0 0.5 1 1.5 2 2.5 3 3.5 4 .V (Em) Answer the following questions. 8. Look at your data table and graphs. Are the theoretical values and underestimate or an overestimate of the experimental values? 9. The innite line charge equation is a valid approximation for a nite line charge if the points are close to the line charge. \"Close\" means the y coordinate of the point is much smaller than the length of the charge distribution. Mathematically, this means y dx ( L+ d -x ) z constants de = [L ( Ltd - x ) = - dx o E = Ked dx Jo ( L + d - x ) 2 E = Ked ( 12) E = Kex - - + 146 E = Ked alltd ) E E = Kel L d ( Ltd ) * = Q , Q = total charge L E = K. Q in terms of Q d ( L+d ) what if P was very far away from the rod so that d approaches infinity d -+ 00 E = K. Q Lim ( L + d ) = d d( L+d ) E = electric field formula for a point charge very far away, the rod looks like a point charge rod behaves like a point charge when you are far away from it E = K. Q d ( L+d ) Electric Field - Distributed Charges Page 2let's look at the case where the rod gets very short: as _ approaches zero lim L - 0 (L+ d) = d E = K Q point charge formula d z rod behaves like a point charge as its length gets small Charged Thin Rings - 1D in Polar Coordinates (r, e ) Find the field at the center of the ring. 1 = constant as = are length R da - charge R de T In length ds ds = R do do= ads da = > Rdo ID , polar coordinates from symmetry, de , and dE, are equal / opposite they cancel out de, X this means that the net field at the center is zero Find the electric field at P for a uniformly charged thin half-ring with radius R and constant linear density 1. dq = ARde aq = 1 kdo t dE, cancels out + so the net field is in the -k direction P X de = K. dy dEz de de r = R for all da, Enet so r = constant = R de = ke da dq = 2 R do R Z dE = Kel Rde R de = Kerde R dE? = - dE sine dEz = - dEsine dey Electric Field - Distributed Charges Page 3dez = - de sine ( dEz = - dEsine dEy dex de - Ke ) de sino 0 R E, = - Ked Sin e de R = +ked R Ex : Ke d Cos TI - Cos 0 ) R Ex = Kel ( - 1 - 1 ) R Ex = - 2ked R R 1 = Q length TR E = 2 K, Q TIRE * = constant E = 2 K, Q TIR semis circle, uniform density, field at center of curvature Finding E for a ring, uniform 1, a distance d above center N de d - X components in the xy plane cancel out so E is in the z direction d = constant thin ring, uniform density, field a distance d above the plane of the ring E = Ke Q d ( R2 + d2 ) 3/2Now to 2D (area charge distribution, o) dq = o dA d dov R y solid disk is made of concentric thin rings the total field is just the sum of the fields by the thin rings dq - .. . ... each ring produces a field in the z direction P E = 20KT - d ( R 2 + d R Circular disk with o= constant, with radius R, a distance d above center let's' look at a disk with R - co so we have an infinite plane E ( infinite plane) = Lim 20 K, T Lim R + d 2 = R2 ) = R = DO O R 2 + 8 2 E ( co plane ) = 25 ke TT = constant note that d drops out d is the distance from the plane 11711 111 11 E = constant E = constant 111 11 11711 E = constant E = constant E 1 plane Electric Field - Distributed Charges Page SE= constant E + plane 11 1 1 111 11 111 11 edge effects for a real (non-infinite) plane, there are edge effects where E is no longer constant !! !!! let's look at points as we get very near to the plane or as d - 0 E = 25 K TT /1 Lim d-0 a 0 E(near a plane ) = 20 ke TT T = constant Electric Field - Distributed Charges Example Problem PHYS 421 First /Last Names 1. Two infinite planes are arranged so that one is the xz plane and the other is the xy plane. See figure. (a) Find the net electric field at (0, d, d). Give answer in vector notation. we will use superposition find E for positive plane Electric Field - Distributed Charges Page 6E (- k ) * 20 y E . = 2 ( 20 ) ke 7 1 E , = - 20 kell K = 40 Ke TIj my Enet = Hoke Tin - 20 Ke TT K E (o , d , d ) = 20 Ke TT ( 2 j - K ) (b) Find the net electric field at (0, -d, -d). Give answer in vector notation. 2 Z - +20 y - . . . . . - a E= / 20 KeTT/ 12+k E, = - 2(20 ) Ke TT ; E 2 = 20 Ke TK E, = - 40 kelly E ( D , -d , - d ) = 25 KeTT ( - 2 ; + K ) (c) An electron (the system charge) is placed at (0. d. d). What is the force the infinite planes (the sources) exert on the electron? Give answer in vector notation. E(o , d , d ) = 20 Ke TT ( 2 , - K ) by sources F = 9 sus E 9 sys = - e F on = 20 ke TT ( - 25 + K ) electron - system (d) A proton is placed at (0. -d. -d). What is the force the proton exerts on the infinite planes? Give answer in vector notation. E ( D , -d , - d ) = 20 KeTT ( - 2; + K ) F = 9 sys E 9 sys = e F = 20 ekeTT ( - 2 ; + K ) Electric Field - Distributed Charges Page 7