LEGv8 ASSEMPLY LANGUAGE/ARM

// No Flyover Tower of Hanoi game driver // EOR X1, X1, X1 // initialize the number of moves to 0 // stack pointers for stacks A, B, and C are X5, X6, and X7 // stacks A, B, and C grow upward ADDI X5, XZR, #0 // X5 = 0x0000 ADDI X6, XZR, #128 // X6 = 0x0080 ADDI X7, XZR, #256 // X7 = 0x0100 // place a super large disk (of size 255) at the bottom of each pile ADDI X9, XZR, #0x00ff STUR X9, [X5, #0] STUR X9, [X6, #0] STUR X9, [X7, #0] // store n disks on src pile in the decreasing size order ADDI X0, XZR, #7 // n = 7 ADD X10, XZR, X0 loop: ADDI X5, X5, #8 STUR X10, [X5, #0] SUBI X10, X10, #1 CBNZ X10, loop // pile A = 0 // pile B = 1 // pile C = 2 ADDI X2, XZR, #0 // src = A ADDI X3, XZR, #2 // dst = C ADDI X4, XZR, #1 // tmp = B BL nfhanoi STOP // nfhanoi(n, src, dst, tmp) // simulate no flyover tower of hanoi game // // assume that input n is in X0, src/dst/tmp in X2/X3/X4 // return number of moves in X1 nfhanoi: ///////////////////////////////////////////////////////// // // your code should go here // ///////////////////////////////////////////////////////// BR LR // move(src, dst) // move a disk from src pile to dst pile // // src/dst in X2/X3 // pile A = 0 // pile B = 1 // pile C = 2 // return running count of moves in X1 move: ///////////////////////////////////////////////////////// // // your code should go here // ///////////////////////////////////////////////////////// BR LR // move errors // // use these for debugging // -1 is returned in case of size error // -2 is returned in case of flyover error errorS: SUBI X1, XZR, #1 // size error STOP errorF: SUBI X1, XZR, #2 // fly-over error STOP

NO RUSH PLZ I NEED AN ANSWER IN LEGv8 ASSEMBLY LANGUAGE WITH COMMENTS......AND ALSO THIS IS NOT THE BASIC HANOI TOWER. THIS IS A NO FLYOVE HANOI TOWER......

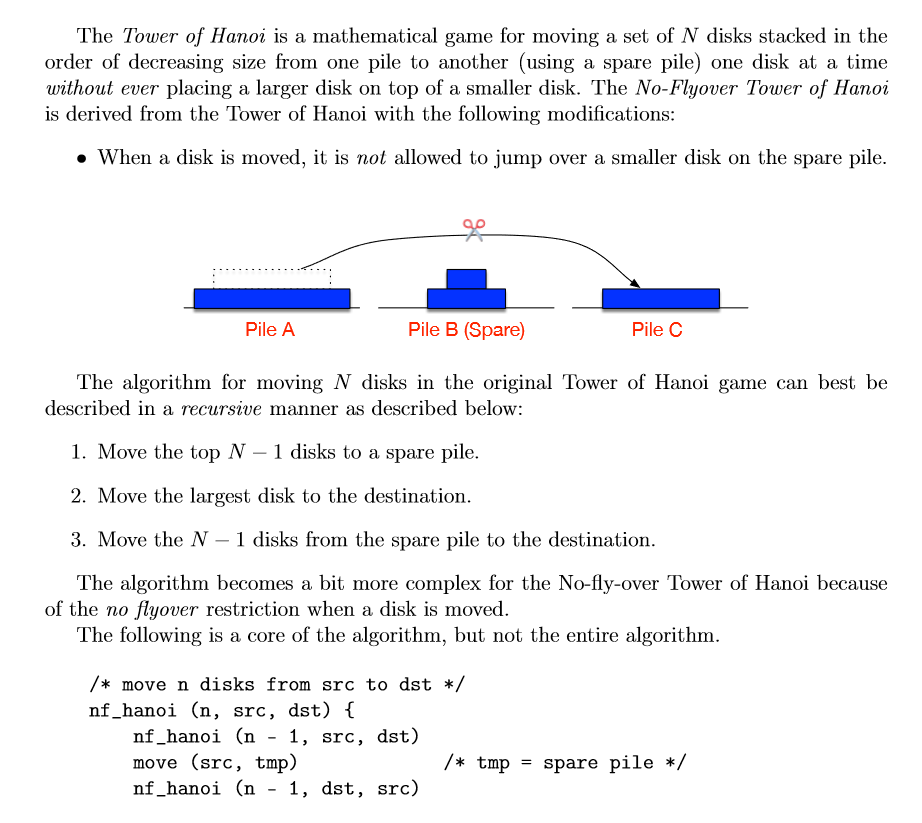
The Tower of Hanoi is a mathematical game for moving a set of N disks stacked in the order of decreasing size from one pile to another (using a spare pile) one disk at a time without ever placing a larger disk on top of a smaller disk. The No-Flyover Tower of Hanoi is derived from the Tower of Hanoi with the following modifications When a disk is moved, it is not allowed to jump over a smaller disk on the spare pile. Pile A Pile B (Spare) Pile C The algorithm for moving N disks in the original Tower of Hanoi game can best be described in a recursive manner as described below 1. Move the top N - 1 disks to a spare pile 2. Move the largest disk to the destination 3. Move the N - 1 disks from the spare pile to the destination The algorithm becomes a bit more complex for the No-fly-over Tower of Hanoi because The following is a core of the algorithm, but not the entire algorithm of the no flyover restriction when a disk is moved /move n disks from src to dst */ nf_hanoi (n, src, dst) nf_hanoi (n - 1, src, dst) move (src, tmp) nf_hanoi (n - 1, dst, src) /* tmp = spare pile */ move (NF Hanoi Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (NF Hanoi) Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (NF Hanol) Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (tmp, dst) nf_hanoi (n - 1, src, dst) The project consists of two parts: (1) to determine the minimum number of moves necessary for moving N disks from pile A to pile C; (2) to simulate the game (the details of which will be discussed in class). Note that the algorithm used for this project must be fully recursive. The number of moves it takes to complete a Tower of Hanoi game in the minimum number of steps can be calculated in a recursive manner as shown below. int hanoi (int n) if (n 1) return 1; else return 2 * hanoi(n-1) + 1 The number of moves required for a no-flyover Tower of Hanoi game would be different but can be calculated in a similar manner or directly from the simulation The following are the specific requirements for the project. 1. The source pile is A and the destination pile C. 2. Piles must be implemented as stacks as shown in Figure 1. The smallest disk is num- bered 1, and the largest N. At the bottom of each pile is a super large disk with size 255, which should not be moved and only exists there for the size comparison purpose. X5, X6, nd x7 are used as stack pointer registers for stacks A, B, and Stacks grow upward from lower memory address to higher. Fach item on the sta should be 8 byte X5 8 X7 Stack A Stack B Stack Figure 1: Piles A, B, and C with N-8. Initially all N disks are stacked on pile A in decreasing size order 3. Moving a disk from a pile to another requires popping an item off a stack and pushing it onto another stack as shown in Figure 2 X5 4 8 X7 Stack A Stack B Stack C Figure 2: A disk is moved from pile A to pile B 4. Figure 3 depicts the final states of the stacks after all of the moves are successfully completed X7 SP X5 SP Stack A Stack B Stack Figure 3: In the final state, all N disks are stacked on pile C in decreasing size order 5. A driver which contains the initial setup for stacks A, B, and C are provided in a separate file: nfhanoi-driver.s. The driver, after initializing the stacks, calls nfhanoi. Inputs to nfhanoi are the number of disks to move, N, and the names of source, destination, and temporary piles: 0 for pile A, 1 for B, and 2 for C. These are passed to nfhanoi via X0, X2, X3, and X4. Thus XO, X2, X3, and X4 contain N, 0, 2 and 1 respectively when nfhanoi is called initially. nfhanoi should return the number of moves made in X1 6. The driver file, nfhanoi-driver.s, includes a template for procedure move as well as helper procedures for debugging: errorS and errorF. move is used to move a disk from a pile to another. Source and destination pile names (again 0 for A, 1 for B, and 2 for C) are passed to procedure move via X2 and X3. move also keeps track of the running count of the total number of moves made and outputs it in X1. errorS and errorF return -1 and -2 respectively in X1 and stops the program execution when a size error or a flyover error has been detected. You should incorporate these two procedures in your code for debugging