Question
Let f [0,1] R be a strictly positive, continuous function. Show that for every positive integer n, there is unique an E (0, 1),
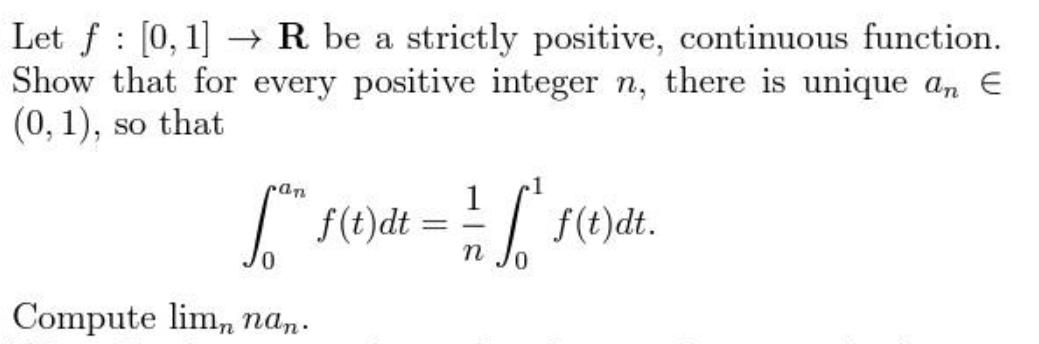
Let f [0,1] R be a strictly positive, continuous function. Show that for every positive integer n, there is unique an E (0, 1), so that an Lo f(t) dt: Compute lim, nan. = 1 n Lo f(t)dt.
Step by Step Solution
There are 3 Steps involved in it
Step: 1
To show the existence and uniqueness of E such that fo ftdt fE we can use the Intermediate Value The...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get StartedRecommended Textbook for
Foundations of Mathematical Economics
Authors: Michael Carter
1st edition
262531925, 978-0262531924
Students also viewed these Mathematics questions
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
View Answer in SolutionInn App



