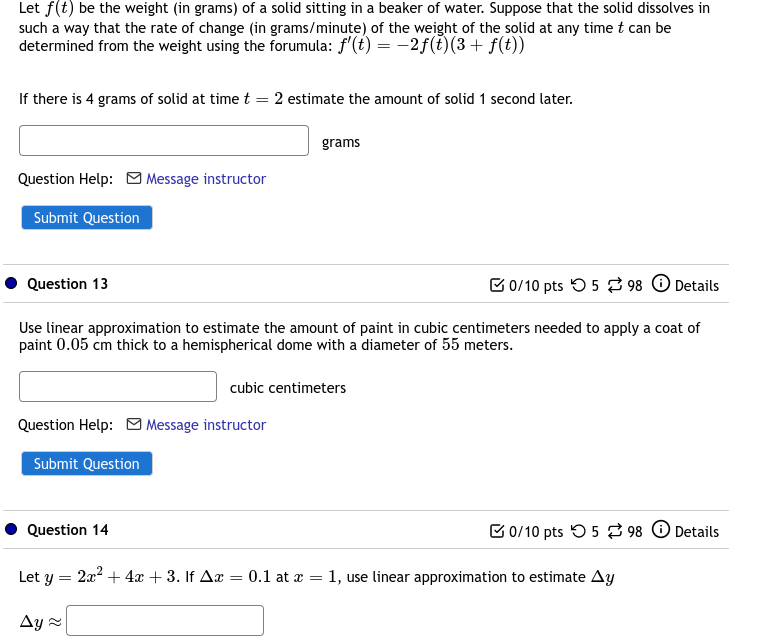
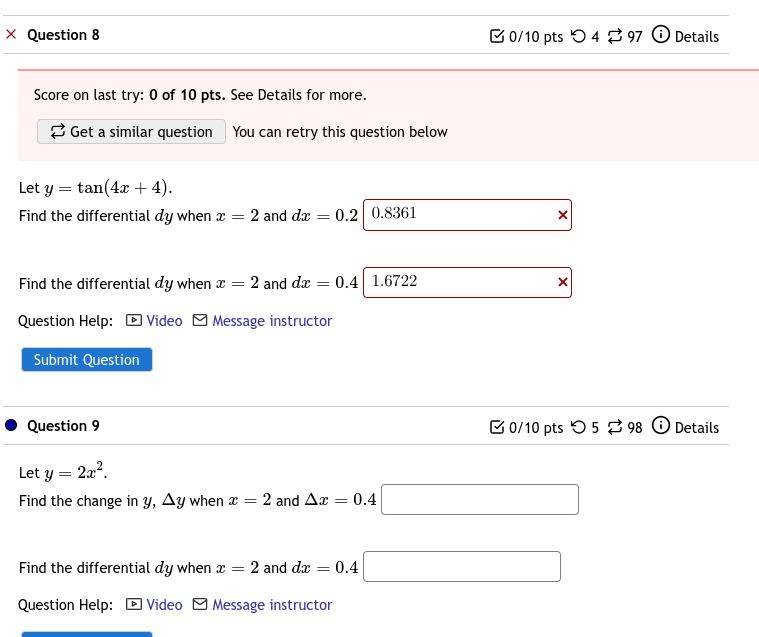
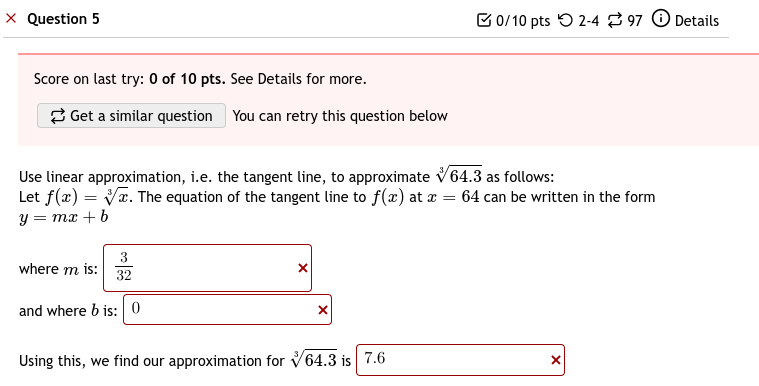
Let f(t) be the weight (in grams) of a solid sitting in a beaker of water. Suppose that the solid dissolves in such a way that the rate of change (in grams/minute) of the weight of the solid at any time t can be determined from the weight using the forumula: f'(t) = 2f(t) (3 + f(t)) If there is 4 grams of solid at time t = 2 estimate the amount of solid 1 second later. Question Help: Message instructor Submit Question grams Question 13 0/10 pts 598 Details Use linear approximation to estimate the amount of paint in cubic centimeters needed to apply a coat of paint 0.05 cm thick to a hemispherical dome with a diameter of 55 meters. cubic centimeters Question Help: Message instructor Submit Question Question 14 0/10 pts 598 Details = Let y 2x+4x+3. If Ax = 0.1 at x = 1, use linear approximation to estimate Ay Ay Question 8 Score on last try: 0 of 10 pts. See Details for more. Get a similar question You can retry this question below Let y tan(4x+4). Find the differential dy when x = 2 and da == 0.2 0.8361 Find the differential dy when x = 2 and dx = 0.4 1.6722 Question Help: Video Message instructor Submit Question Question 9 Let y = 2x. Find the change in y, Ay when x = 2 and Ax == 0.4 Find the differential dy when x = 2 and da = 0.4 Question Help: Video Message instructor 0/10 pts 497 Details 0/10 pts 598 Details Question 5 Score on last try: 0 of 10 pts. See Details for more. Get a similar question You can retry this question below 0/10 pts 2-4 97 Details Use linear approximation, i.e. the tangent line, to approximate 64.3 as follows: Let f(x)=. The equation of the tangent line to f(x) at x = 64 can be written in the form y = mx + b where m is: 3 32 and where b is: 0 x Using this, we find our approximation for 64.3 is 7.6 Question 3 0/10 pts 597 Details 1 1 as follows: Let f(x) = = and 0.104 Use linear approximation, i.e. the tangent line, to approximate find the equation of the tangent line to f(x) at a "nice" point near 0.104. Then use this to approximate 1 0.104 ..