Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Let G act on a non-empty set A. Prove that if a, b E A and b = g.a for some g = G,
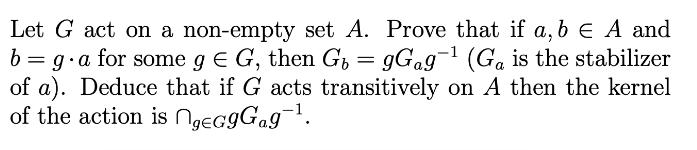
Let G act on a non-empty set A. Prove that if a, b E A and b = g.a for some g = G, then Gb = gGag- (Ga is the stabilizer of a). Deduce that if G acts transitively on A then the kernel of the action is ngeGgGag-.
Step by Step Solution
★★★★★
3.44 Rating (151 Votes )
There are 3 Steps involved in it
Step: 1
Proof Let a and b be two elements in A such that b ga for some g G We need to show that G gGag First ...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Discrete and Combinatorial Mathematics An Applied Introduction
Authors: Ralph P. Grimaldi
5th edition
201726343, 978-0201726343
