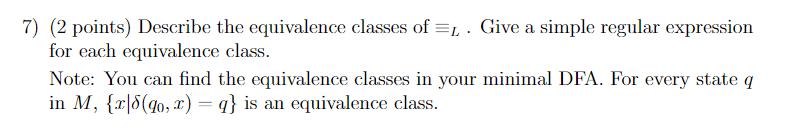
Let L be the language over {a,b} described by: aa*bb* Ub*. 1) (4 points )Draw a minimal DFA M for L. (Note: if your DFA is not minimal, it will become clear below when you try to show and can't - that all the strings in your index set X are pairwise distinguishable.) 2) (1 point) How many states does a minimal DFA for L have? 3) (1 point) What is the value of the index of L? 4) (1 point) How many equivalence classes does = have? 5) (2 points) Give a largest set X of strings that is pairwise distinguishable by L. (Note: You can read these off from your minimal DFA. For every state q in M, put one string x with 8(qo, x) = q in X.) 6) (3 points) Show that X is pairwise distinguishable by L (List every pair and show the distinguishability). 7) (2 points) Describe the equivalence classes of L. Give a simple regular expression for each equivalence class. Note: You can find the equivalence classes in your minimal DFA. For every state q in M, {x|8(90, x) = q} is an equivalence class.