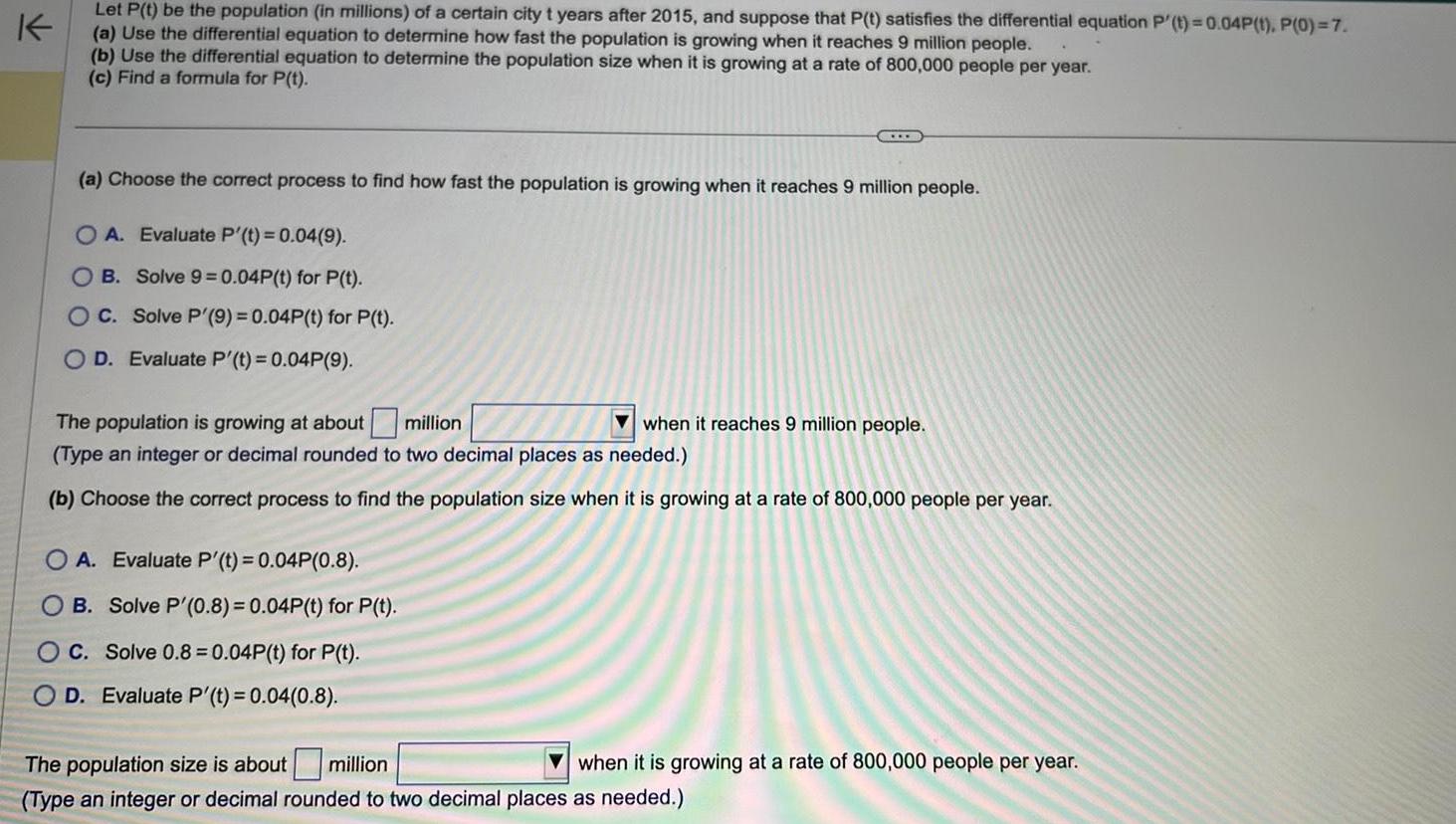
Let P(t) be the population (in millions) of a certain city t years after 2015, and suppose that P(t) satisfies the differential equation P'(t)=0.04P(1), P(0)=7. (a) Use the differential equation to determine how fast the population is growing when it reaches 9 million people. (b) Use the differential equation to determine the population size when it is growing at a rate of 800,000 people per year. (c) Find a formula for P(t). (a) Choose the correct process to find how fast the population is growing when it reaches 9 million people. OA. Evaluate P'(t)=0.04(9). OB. Solve 9=0.04P(t) for P(t). OC. Solve P'(9) = 0.04P(t) for P(t). OD. Evaluate P'(t) = 0.04P(9). The population is growing at about million when it reaches 9 million people. (Type an integer or decimal rounded to two decimal places as needed.) (b) Choose the correct process to find the population size when it is growing at a rate of 800,000 people per year. OA. Evaluate P'(t)=0.04P(0.8). OB. Solve P'(0.8)=0.04P(t) for P(t). OC. Solve 0.8 0.04P(t) for P(t). OD. Evaluate P'(t)=0.04(0.8). The population size is about million when it is growing at a rate of 800,000 people per year. (Type an integer or decimal rounded to two decimal places as needed.)