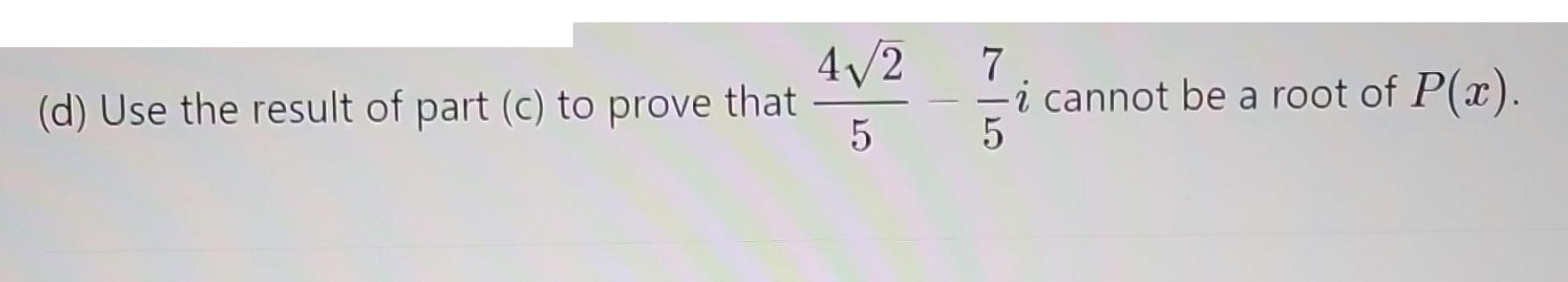
Let P(x) = 10x7 - 2x + 5x5 + x - 7x - 1. (a) Find the possible number of positive real zeros of P(x). (b) Use Descartes' Rules of Signs to show that 1 2 cannot be a zero of P(x). (c) Given that the Bounds Theorem holds for the complex roots if one interprets co as the modulus of o, find an upper bound on moduli of the roots of P(x). (d) Use the result of part (c) to prove that 42 5 7 i cannot be a root of P(x). 5