Let the utility function of an agent born at time t 1 be given by U= lnc_1,t + lnc_2,t+1 and this agents endowment be (1, 0) so that y = 1 for convenience. Let the production function for capital be given by f(k_t) = 2k_t^1/2 . Assume that the population grows at the rate n = 2 and that capital is the only form of saving. a. Since we have that c_1,t 1and c_2,t+1 2k_t^1/2 , solve the young agents utility maximization problem and verify that the solutions to this problem are

c_1,t =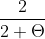 , c_2,t+1 = 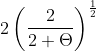, k_t = 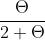b. Show mathematically that the equilibrium rate of return to capital is given by f^'(k_t)= 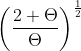c. Let = 1 . Determine if this economy is overcapitalized or undercapitalized. Given your answer, is the equilibrium allocation dynamic efficient or dynamically inefficient. Briefly explain your reasoning. d. Let = 1/2 . Determine if this economy is overcapitalized or undercapitalized. Given your answer, is the equilibrium allocation dynamic efficient or dynamically inefficient. Briefly explain your reasoning. e. Solve for the value of for which the equilibrium allocation will achieve the Golden rule allocation.