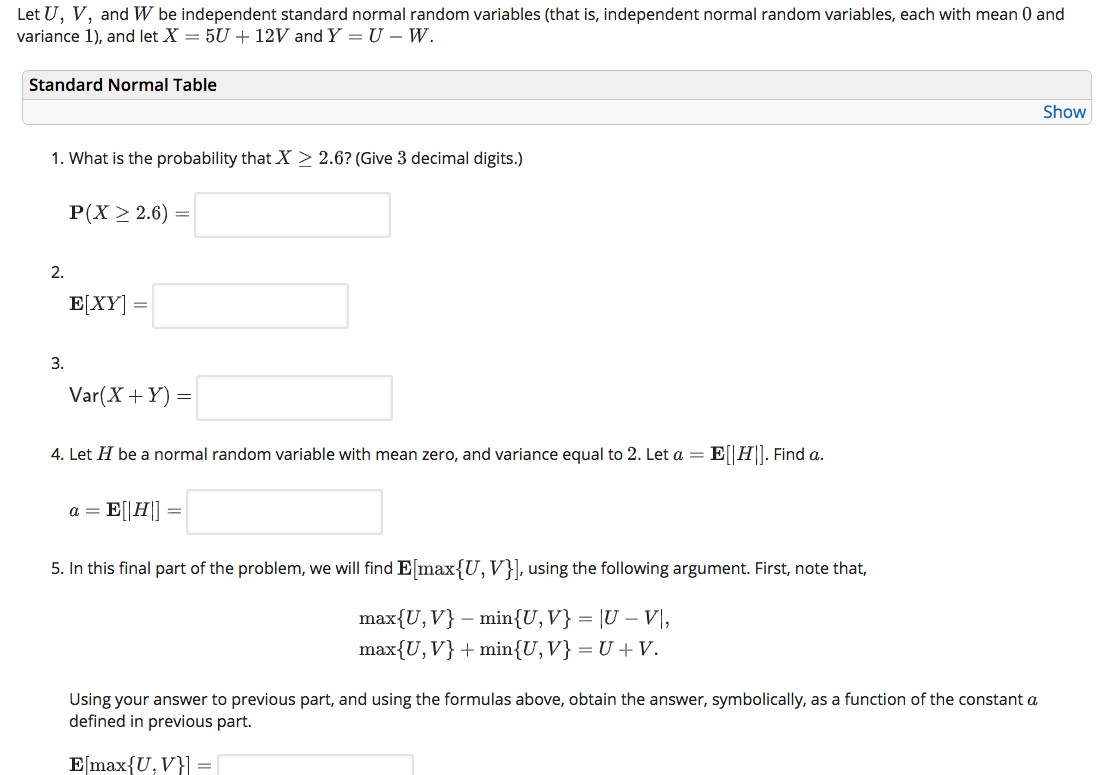
Let U, V, and W be independent standard normal random variables (that is, independent normal random variables, each with mean 0 and variance 1), and let X = 5U + 12V and Y = U - W. Standard Normal Table 1. What is the probability that X > 2.6? (Give 3 decimal digits.) P(X2.6) = 2. 3. E[XY] = = Var(X + Y)= 4. Let H be a normal random variable with mean zero, and variance equal to 2. Let a = E[|H|]. Find a. a = E[|H|] = 5. In this final part of the problem, we will find E[max{U, V}], using the following argument. First, note that, max{U, V}-min{U, V} = |U V], max{U, V)+ min{U, V} U+V. Using your answer to previous part, and using the formulas above, obtain the answer, symbolically, as a function of the constant a defined in previous part. Emax(U, V Show