Question: Let V be a vector space of dimension n, and let W, W2 be subspaces of V. (a) Assume that W W = {0}.

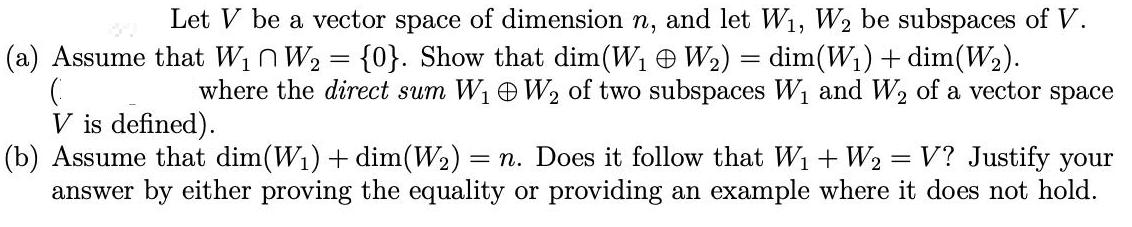
Let V be a vector space of dimension n, and let W,

Let V be a vector space of dimension n, and let W, W2 be subspaces of V. (a) Assume that W W = {0}. Show that dim(W W) = dim(W) + dim(W). ( where the direct sum W W of two subspaces W and W of a vector space V is defined). (b) Assume that dim(W) + dim(W) = n. Does it follow that W + W = V? Justify your answer by either proving the equality or providing an example where it does not hold.

Step by Step Solution

★★★★★

3.38 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To show that dimW W dimW dimW when W W 0 we can use the ranknullity theorem By definition W W is t... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 30 37 38 39 40 41 42 43 44 45 40 47 48 49 50 51 52 53 54 55 1 In the last 10 years, Victoria has worked for Alberta...

Let V be a vector space with subspaces U and W. Define the s u m of U a n d W to be U + W = {u + w: u is in U, w is in W} (a) If V = R3, U is the x-axis, and W is the y-axis, what is U + W? (b) If U...

Let V be a vector space with subspaces U and W. Give an example with v = [R2 to show that U U W need not be a subspace of V.

Let V be a vector space with subspaces U and W. Prove multiplication that U W is a subspace of V.

Redesign the system in Problem 6.14 with the following equipment: The owner of a small cabin would like to convert her home to PV power. She has the following equipment and associated run times: PV...

The homeowner decides to hire you to design a system for her. She has arranged with a local solar supplier for the following equipment. Specify the system and provide a line diagram. The owner of a...

Investigation 3 Activity 3 3.2: Same Molecules but Different Representations Scientists develop and use molecular models for a variety of reasons. One reason is that molecular models help scientists...

Consider a model with two countries called France and Germany. France has one automaker, called Citroen. Germany has a competitor company, called Volkswagen. Citroen can produce cars at a constant...

Define and explain the global counter flow argument as discussed in the lecture. Next summarize a recent (since 2018) example of global counter flow. Finally, point out a limitation of global counter...

Suppose your top drawer contains different colored socks 8 are white 6 are black 14 are pink and 4 are blue All socks in the drawer are loose unpaired In the morning you randomly select two socks one...

Question 1 (Multiple Choice Worth 7 points) (07.01) In a city school of 900 students, 30% of the students are on the honor roll, 70% have a part-time job, and 25% are on the honor roll and have a...

Aylmer Inc has a December 31, 2022 year end. Aylmer does not perform monthly adjusting entries. The following items relate to transactions that occurred during the year. 1 On August 1, Aylmer paid...

Marvin industries Inc. operates as a diversified software company worldwide. Its Digital Media segment provides tools and solutions that enable individuals, teams, and organizations to create,...

Question 3 0 ( 1 point ) Marvin purchased a large plece of land 5 years age when a highway bypas was rumored to have on exit beling buil nearby. He had planned to subdlide the land info bulding lots...

Using the following independent situations, answer the following questions: Situation # 1 Clara received from her Aunt Sona property with a FMV at the date of the gift of $40,000. Aunt Sona purchased...

Southern Copper Corporation (PCU) acquired mining equipment for $100,000 cash on January 1, 2009. The equipment had an expected useful life of four years and zero salvage value . PCU calculates...

The following independent situations relate to inventory accounting: 1. Draper Co. purchased goods with a list price of $175,000 and a trade discount of 20% based on the quantity purchased, with...

Zachery Neel and Lauren Tate formed a limited liability company with an operating agreement that provided a salary allowance of $45,000 and $30,000 to each member, respectively. In addition, the...

Consider a sample with data values of 10, 20, 12, 17, and 16. Compute the range and interquartile range.

The Financial Action Task Force (FATF), under the leadership of the Mexican presidency, recently published important new amendments to the FATF Recommendations. These amendments are aimed at...

Let V be the vector space of Problem 29 and let the subset W consist of those elements {x n ) of V such that X n = X n-1 + X n-2 for n 2. Thus a typical element of W is the Fibonacci sequence (a)...

Let U and W be subspaces of a finite-dimensional vector space V. Prove Grassmann's Identity: dim ( U + W) = dim U + dim W - dim( U W)

3. Let L: V W be an isomorphism of vector spaces. Prove each of the following statements to show that L respects dimension, both of subspaces and of cosets, and the affine incidence structure in V...

1. Determine which of the following sets form a basis of the respective vector spaces and justify your answer: (a) {4t 2t+3,6t t +4, 8t - 8t+7} of P2(R), the vector space of polynomials in t - over R...

(Requires the subsection on Combining Subspaces, which is optional.) Let U and W be vector spaces. Define a new vector space, consisting of the set U Ã W = {(, ) | U and W} along with these...

Math 636 Midterm Quiz \u001a\u0014 \u0015 \u001b x1 2 1. The geometric interpretation of the following set W = R | x1 + x2 = 2 is x2 (a) a point in R2 . (b) a line in R2 passing through the origin....