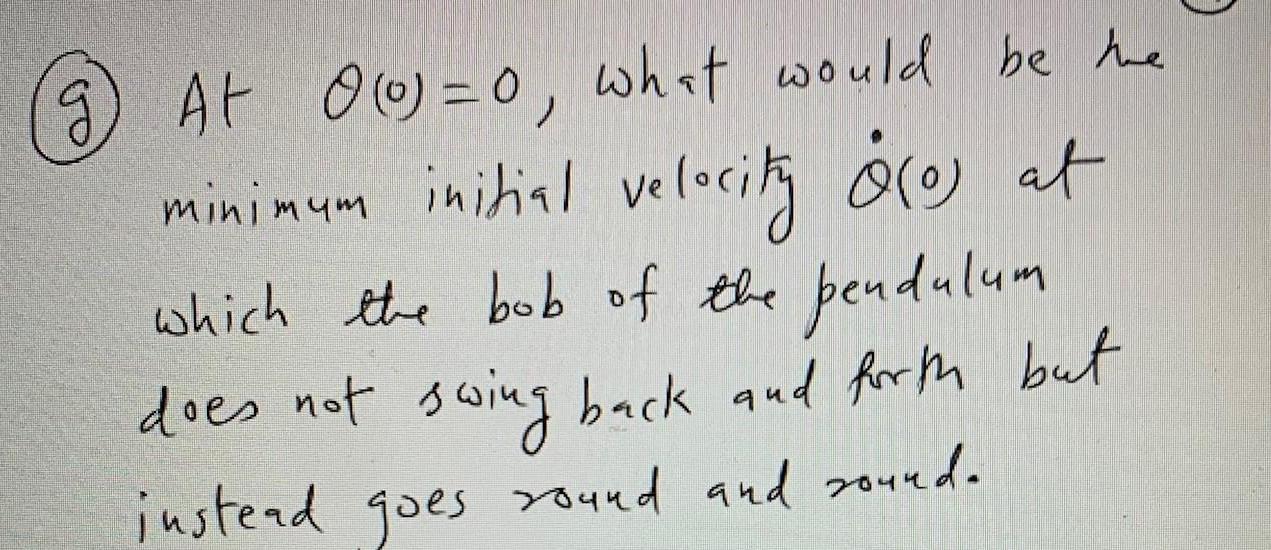
Let x 1 =%2 = - 12 sinx, be the nonlinear equation of a simple pendulum @ where [Tell m. of the pendudum ? the equilibrium points me * where the r.h.s. of is zero ] (6) Linearize in the vicinity of (0,0) and write down an equation similar F (9.8). X = MX What is M? Oi) write down the eigenvalues and eigenvectors of M from part 6. (ii) Now write down the solution vectors. X, (t) and X (t) tom podt for the linear dynamics & = MX. (ii) Hence write down the generel solution 8(t) = @ Taking the linear dynamies in part 6 write down the equation of the ellipse [see (9.30), in the notes]. indicating the Plot this ellipse direction of the phase porbait. [see Fig 19, in Lec notes] using phase plane Amethod from page 9.32) Le notes 9 derive an equation similar to (9.46). [Choose Xo =1 and play in the value of 9/] Now plot a phase portrait similar to the green curre on Fig 23 in Lec Notes 9. This will be a plot of Eq. (9.46). g) At 00=0, what would be the minimum initial velocity ore at which the bob of the pendulum does not swing back and forth but instead goes round and sound. (B) we now add friction to our pendulum equation. is "1 = "1. * 2 = -12 sinxe, -2x12. The new equation (9.52) in Lec Notes 9. X = MX. (h) Linearize () using Taylor's expansion in the vicinity of x = x = 0, and write down an equation similar to write down M. L ** otiw (2) Calculate the two complex eigenvalues, of M. What are & and W for mis problem. 4 (j) Now calculate the complex eigenvector for the eigenvalue o+iw. (k) write down the solution vectors. X (t), X(t). Also write down the general solution X (t) = term as in (1) Ignoring the est (9.58) and define 57, (t, (t), write them down. Eliminating sinot and cos ats derive the ellipse as in (9.59). write down equation of this ellipse (m) Using what you have learnt in Lec 4, sketch the ellipse in part (1) Compute '2, 'a' and 'b' for this problem. Don't forget to show the direction of the phase brajectory, on on this sketch.