Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Let (xn)neN be a sequence in an ordered field. Prove that: a) Liminf x_n=-Limsup(-x_n) b) and that the largest accumulation point of (xn)neN is
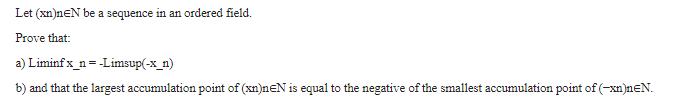
Let (xn)neN be a sequence in an ordered field. Prove that: a) Liminf x_n=-Limsup(-x_n) b) and that the largest accumulation point of (xn)neN is equal to the negative of the smallest accumulation point of (-xn)neN.
Step by Step Solution
★★★★★
3.41 Rating (157 Votes )
There are 3 Steps involved in it
Step: 1
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Elementary Linear Algebra with Applications
Authors: Bernard Kolman, David Hill
9th edition
132296543, 978-0132296540
