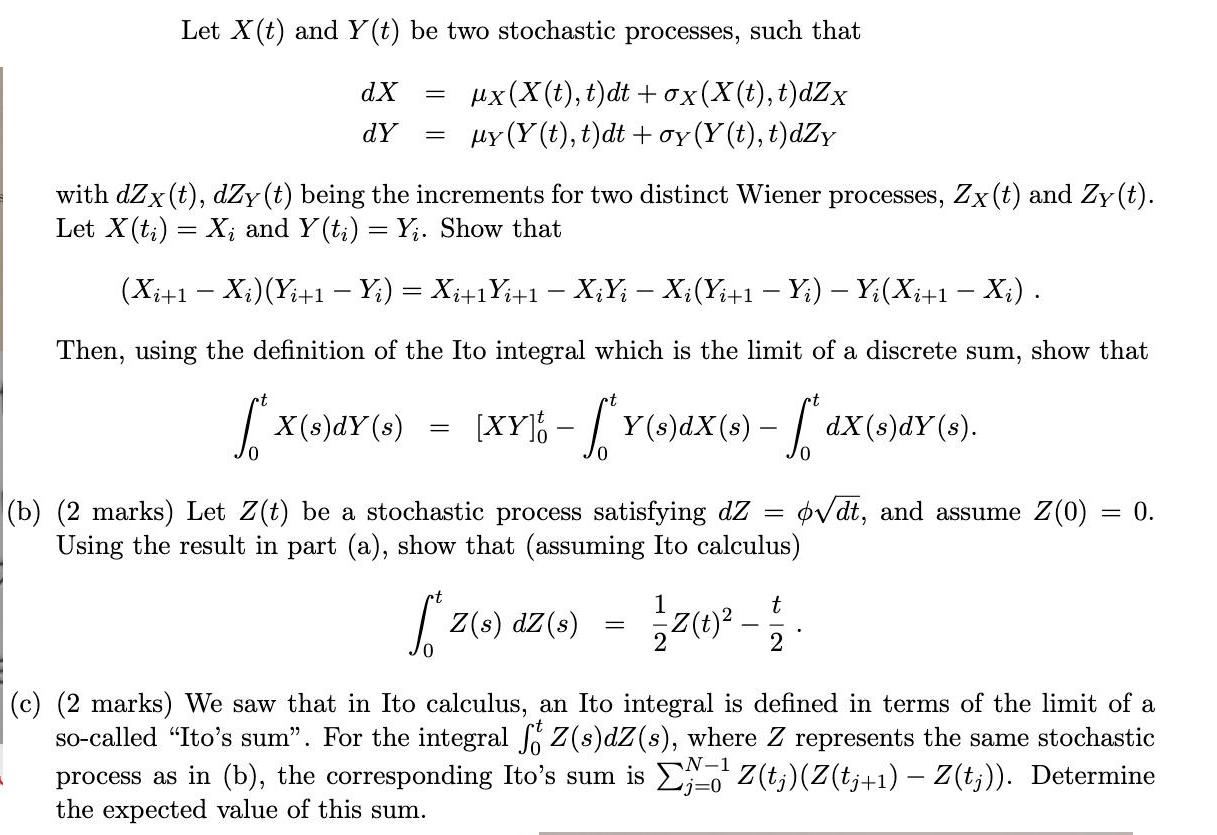
Let X(t) and Y(t) be two stochastic processes, such that dX dY = = ux(x(t), t)dt+ox(x(t), t)dZx y (Y(t), t)dtoy (Y(t), t)dZy with dZx(t), dZy (t) being the increments for two distinct Wiener processes, Zx(t) and Zy(t). Let X(t) = X and Y(ti) = Yi. Show that - - (Xi+1 Xi)(Yi+1 Yi) = Xi+1Yi+1 - XiYi - Xi(Yi+1 - Yi) - Yi(Xi+1 - Xi). Then, using the definition of the Ito integral which is the limit of a discrete sum, show that [XY-Y(s)X(s) - dX(s)dY(s). X(s)dY(s) = (b) (2 marks) Let Z(t) be a stochastic process satisfying dZ = Using the result in part (a), show that (assuming Ito calculus) odt, and assume Z(0) = 0. Z(s) dZ (s) 1 t = - 2 (c) (2 marks) We saw that in Ito calculus, an Ito integral is defined in terms of the limit of a so-called "Ito's sum". For the integral ft Z(s)dZ(s), where Z represents the same stochastic process as in (b), the corresponding Ito's sum is Z(t;) (Z(tj+1) - Z(t;)). Determine the expected value of this sum. N-1