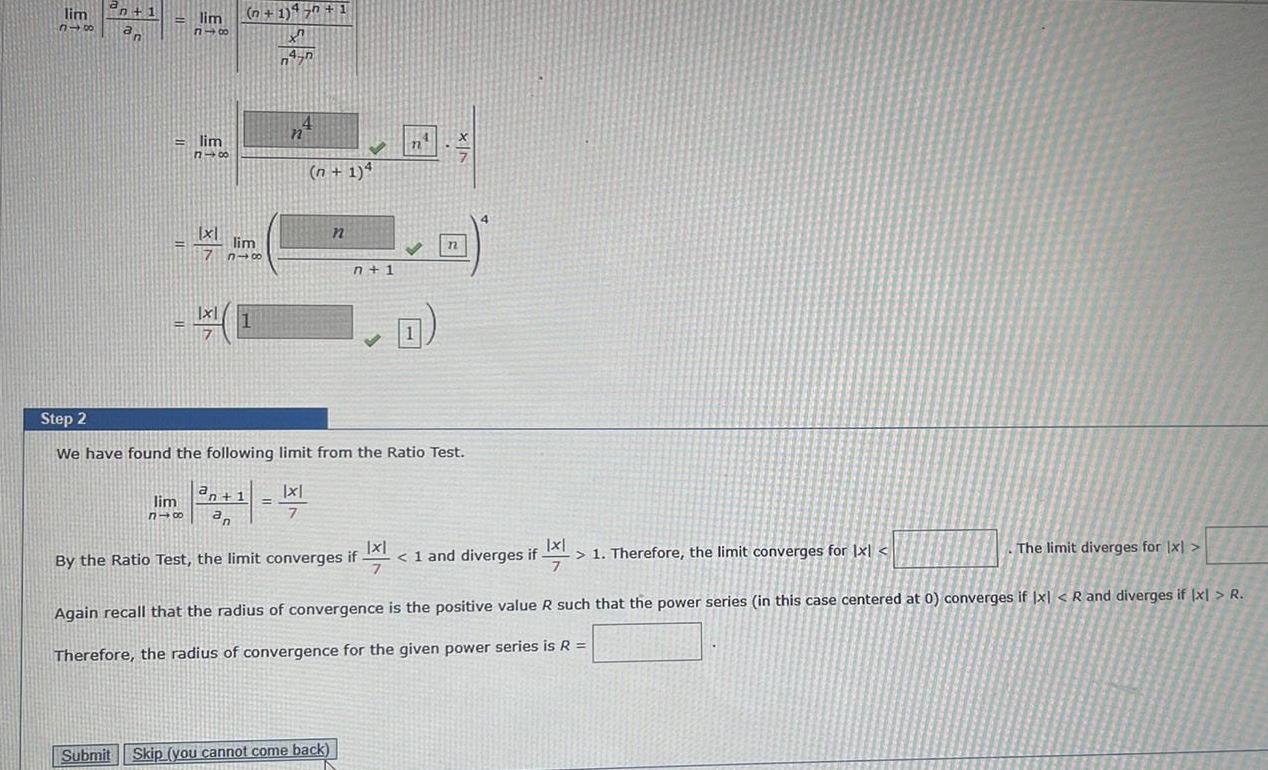
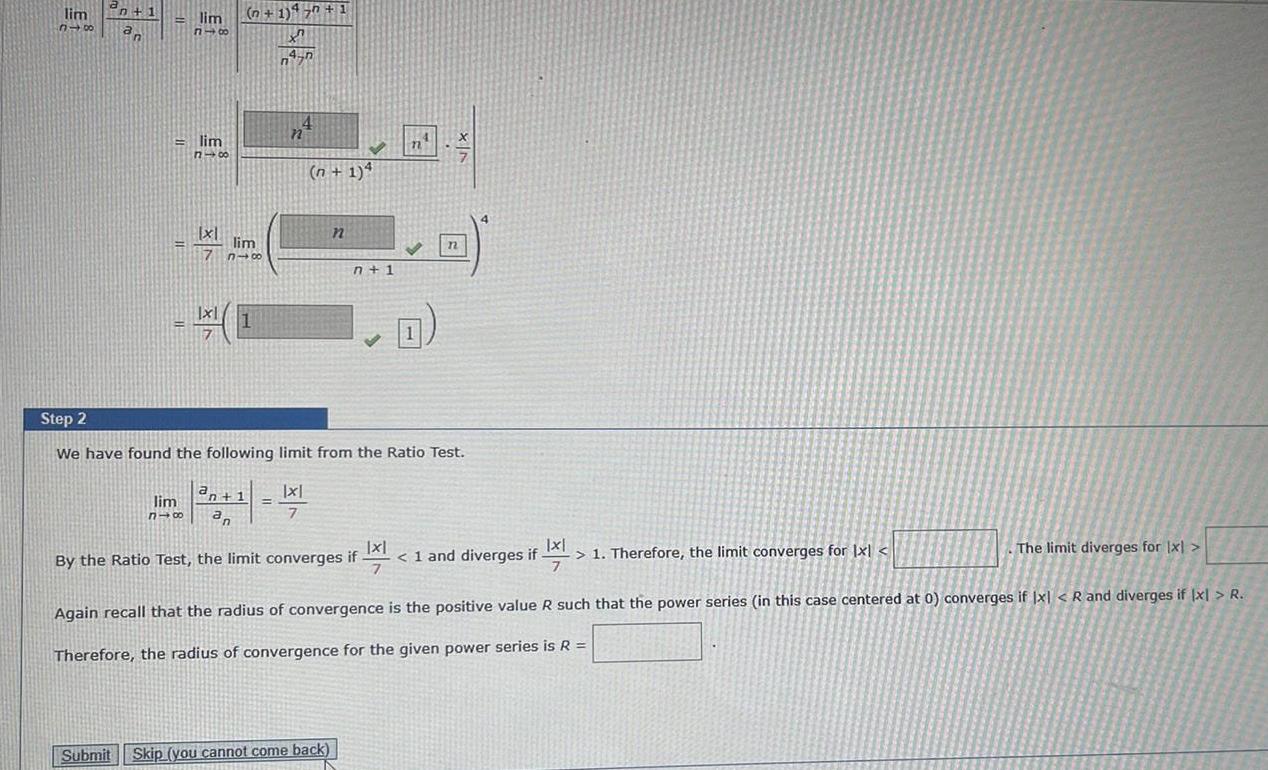
lim 318 n 1 an lim 816 lim 818 x1 7 n 1 450 1 X 4 n n lim n 1 a n 1 lim 818 an 4 n n 1 4 Step 2 We have found the following limit from the Ratio Test x 7 n n 1 Submit Skip you cannot come back 71 By the Ratio Test the limit converges if Q n x FIX 1 and diverges if 1 Therefore the limit converges for Ixl if 21 The limit diverges for x Again recall that the radius of convergence is the positive value R such that the power series in this case centered at 0 converges if x R and diverges if x R Therefore the radius of convergence for the given power series is R