Longest path in 2D Array:

import java.io.BufferedReader;

import java.io.InputStreamReader;

import java.util.ArrayList;

import java.io.IOException;

import java.util.HashMap;

import java.lang.Math.abs;

class NonDecreasing {

/**

* Take a rectangular grid of numbers and find the length

* of the longest sub-sequence.

* @return the length as an integer.

*/

public static int longestSequence(int[][] grid) {

// YOUR ANSWER HERE

}

public static void main(String[] args) throws IOException {

BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

int numRows = 0;

int numCols = 0;

String[] firstLine = reader.readLine().split("\\s+");

numRows = Integer.parseInt(firstLine[0]);

numCols = Integer.parseInt(firstLine[1]);

int[][] grid = new int[numRows][numCols];

for (int row = 0; row

String[] inputRow = reader.readLine().split("\\s+");

for (int col = 0; col

grid[row][col] = Integer.parseInt(inputRow[col]);

}

}

int length = longestSequence(grid);

System.out.println(length);

}

}

// I don't fully understand how standard input/output work, so if you could include a 1-2 sentence explanation, that would great!

Thank you!

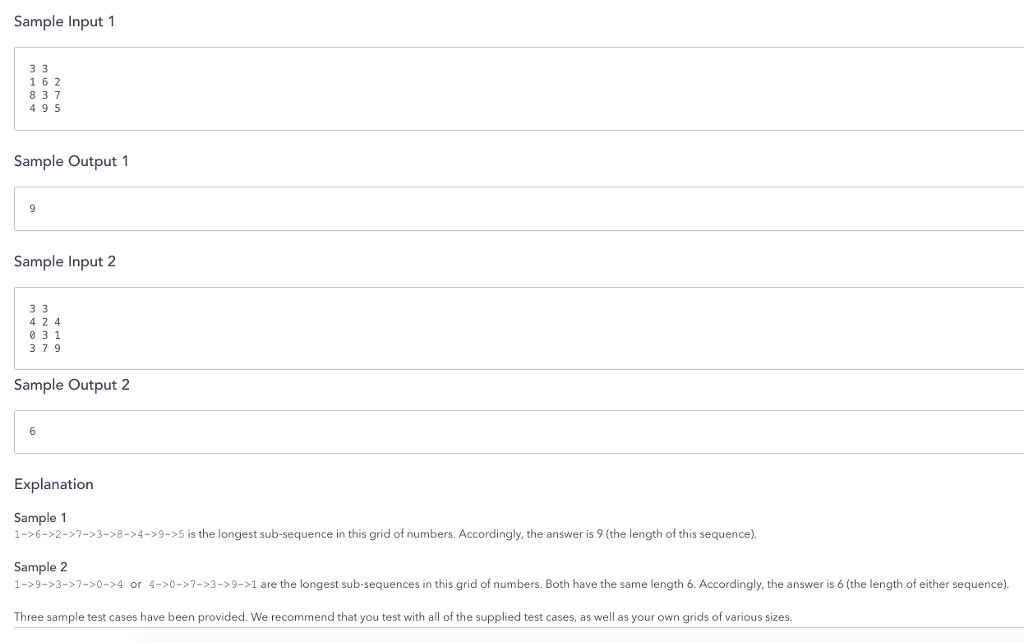
Problem Statement Find the length of the longest of a special sub-sequence as defined below through adjacent,non-repeating cells (including diagonals) in a rectangular grid of numbers. The special sub-sequence is defined such that the difference between the current and next value in the sub-sequence is greater than 3. For example, in the following grid, one legal path (though not the longest) that can be traced is o-6-2-8 and its length is 4 3 79 The path can only connect adjacent locations (including diagonals) and cells may not be repeated. For the example above, you cannot connect 8-3 but you can connect 7-1. The longest possible sub-sequence for this example would be oflength 8 by tracing the path 9->1->6-2->8-0->7->3 Task In the language of your choice, write a program that takes a rectangular grid of numbers as input and returns the length of the longest such sub-sequence as output Input will be given on STDIN and utputll be read from STDOUT. Code that reads the grid from STDIN and writes to STOOUT has been provided for many languages. Input Format The first line of input contains two space delimited integers R. c. These numbers denote the number of rows (R) and columns (C) in the grid The next R lines of input contain C space delimited integers. All together, these represent the grid. Constraints Output Format In a single line, output the length of the longest special sub-sequence Problem Statement Find the length of the longest of a special sub-sequence as defined below through adjacent,non-repeating cells (including diagonals) in a rectangular grid of numbers. The special sub-sequence is defined such that the difference between the current and next value in the sub-sequence is greater than 3. For example, in the following grid, one legal path (though not the longest) that can be traced is o-6-2-8 and its length is 4 3 79 The path can only connect adjacent locations (including diagonals) and cells may not be repeated. For the example above, you cannot connect 8-3 but you can connect 7-1. The longest possible sub-sequence for this example would be oflength 8 by tracing the path 9->1->6-2->8-0->7->3 Task In the language of your choice, write a program that takes a rectangular grid of numbers as input and returns the length of the longest such sub-sequence as output Input will be given on STDIN and utputll be read from STDOUT. Code that reads the grid from STDIN and writes to STOOUT has been provided for many languages. Input Format The first line of input contains two space delimited integers R. c. These numbers denote the number of rows (R) and columns (C) in the grid The next R lines of input contain C space delimited integers. All together, these represent the grid. Constraints Output Format In a single line, output the length of the longest special sub-sequence