Machine: Push Down Automata with 2 Stacks.

Diagram: (Example)

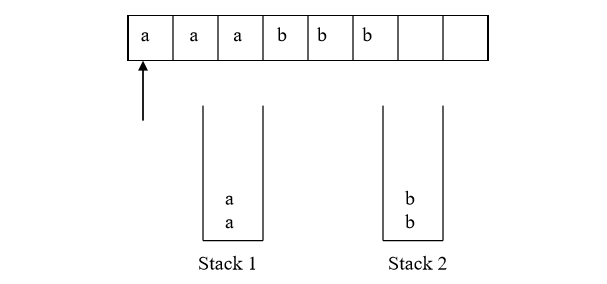
A Push Down Automata (PDA) with two stacks is a Septuple M = (K, , 1, 2, , s, F) K is the finite set of states

is an alphabet (input symbols)

₁ is an alphabet (stack symbols for stack 1)

₂ is an alphabet (stack symbols for stack 2)

s K is the start state

F K is the set of final states

, the transition relation is a finite subset of

(K X ( U {e}) X ₁^*X ₂^*) X (K X ₁^* X ₂^*).

Also, there can be no exchange of symbols between the stacks, i.e., one cannot pop a symbol from stack 1 and push it onto stack 2 and vice versa. This machine that we have designed encompasses all Context-Sensitive languages. We have shown where it falls diagrammatically in the Chomsky hierarchy.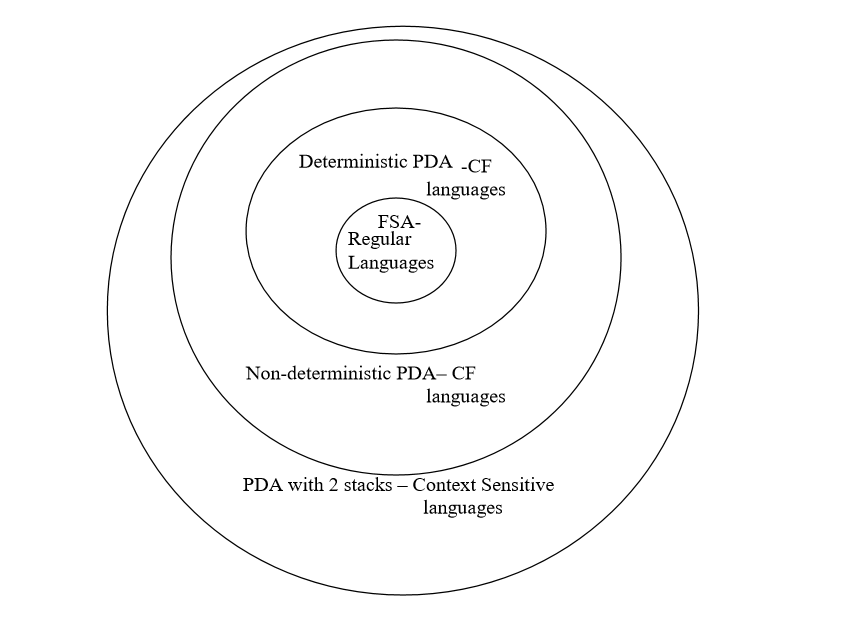

Hence, this machine accepts all regular, context free as well as context sensitive languages. It is not as powerful as a Turing Machine and hence, it cannot accept recursive and recursively enumerable languages. For example, this machine cannot accept the recursive language, L={ ww: w {a, b}^* }, as the symbols in Stack1 and Stack2 cannot be interchanged. We can also think of these machines as algorithms. The states of this machine can be thought of as variables and the input string is the input given to the algorithm and the output for this algorithm would be whether the string is accepted or not. It does this by using the transition functions given in the tuple of the machine. The stacks can be thought of as the data structure that the algorithm uses to perform the transitions specified in the machine. These are three examples of what this machine accepts: 1. Non- Context Free language: {aⁿ b ⁿ c ⁿ: n >= 0) M = (K, , ₁, ₂, , s, F) K = {s, q, f}

= {a, b, c}

₁ = {a}

₂ = {b}

F = {f}

s K is the start state

q K is the intermediate state

F K is the set of final states

= { ((s, a, e, e) , (s, a, e)) ,

((s, b, a, e) , (q, e, b)) ,

((q, b, a, e) , (q, e, b)) ,

((q, c, b, e) , (f, e, e)) ,

((f, c, b, e) , (f, e, e)) } 2. Context Free Language: (This is an example of a context free language that is not regular) {aⁿ bⁿ: n >= 0) M = (K, , ₁, ₂, , s, F) K = {s, f}

= {a, b}

₁ = {a}

₂ = {e}

F = {f}

s K is the start state

F K is the set of final states

= { ((s, a, e, e) , (s, a, e)) ,

((s, b, a, e) , (f, e, e)) ,

((f, b, a, e) , (f, e, e)) } For a context free language, we need to use only one stack and hence it operates in the same way as a regular PDA with one stack.

3. Regular language: {aⁿb : n >= 0) M = (K, , ₁, ₂, , s, F)

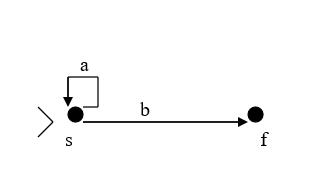
K = {s, q, f}

= {a, b}

₁ = {e}

₂ = {e}

F = {f}

s K is the start state

F K is the set of final states

= { ((s, a, e, e) , (s, e, e)) , ((s, b, e, e) , (q, e, e)) } Hence, we do not need to use any of the stacks for this machine to accept a regular language. In our class of machines, the non-deterministic ones will always be more powerful than the deterministic ones. The non-deterministic machine looks at all possible combinations. When we are looking at context-sensitive languages, there are a large number of possibilities because the input string can be regular, context free or neither. Hence, a non-deterministic PDA with 2 stacks does a good job of accepting as compared to a deterministic PDA. A deterministic PDA may or may not accept all the languages belonging to this class. Now Consider the following Push down automata with two stacks M = (K, , ₁, ₂, , s, F) K = {s, q, f}

= {a, b, c}

₁ = {a}

₂ = {b}

F = {f}

s K is the start state

q K is the intermediate state

F K is the set of final states

= { ((s, a, e, e) , (s, aa, aaa)) ,

((s, b, a, e) , (q, e, e)) ,

((q, b, a, e) , (q, e, e)) ,

((q, c, e, a) , (f, e, e)) ,

((f, c, e, a) , (f, e, e)) } a) Does the string aabbbbcccccc L(m) ? b) Does the string aabbabbcccc L(m) ? 2. Construct a machine based on our definition of a PDA with 2 stacks that accepts the language {w w ^R w: w {a, b}^*}

Stack 1 Stack 2 Deterministic PDA -CF languages FSA- Regular Languages Non-deterministic PDA-CF languages PDA with 2 stacks -Context Sensitive languages