Make a Flowchart for the following code...

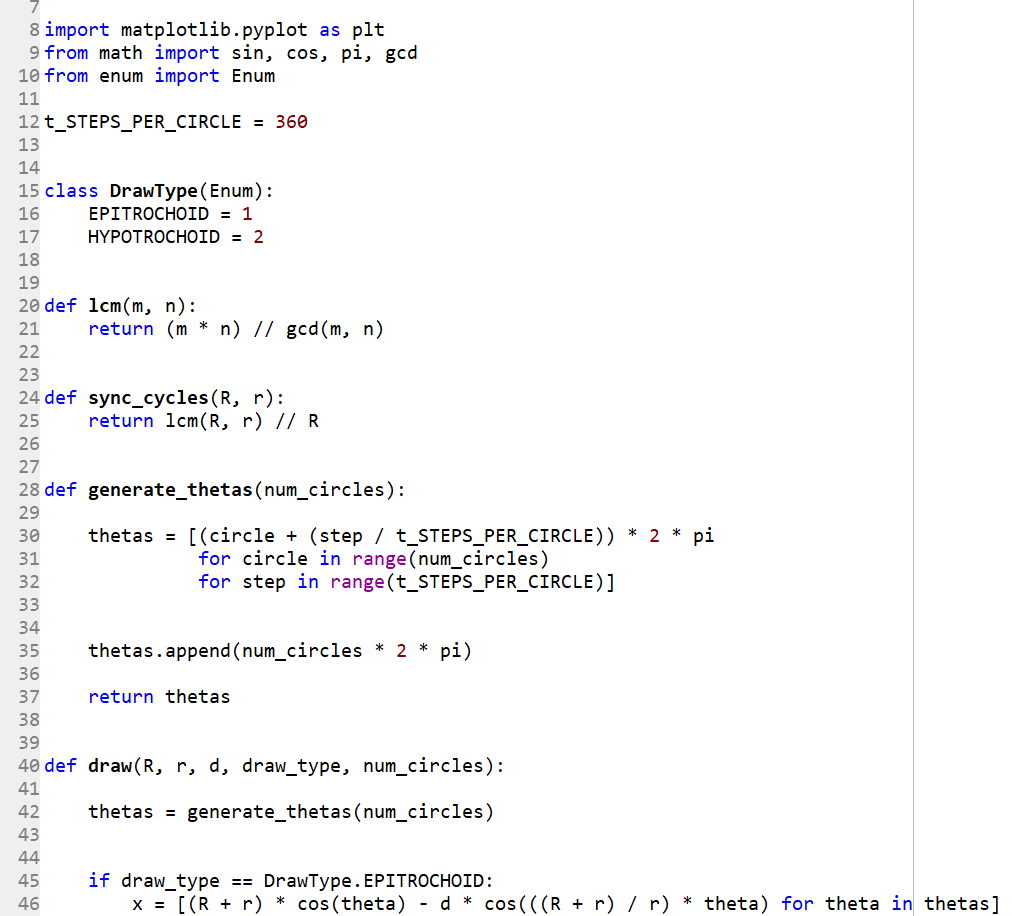
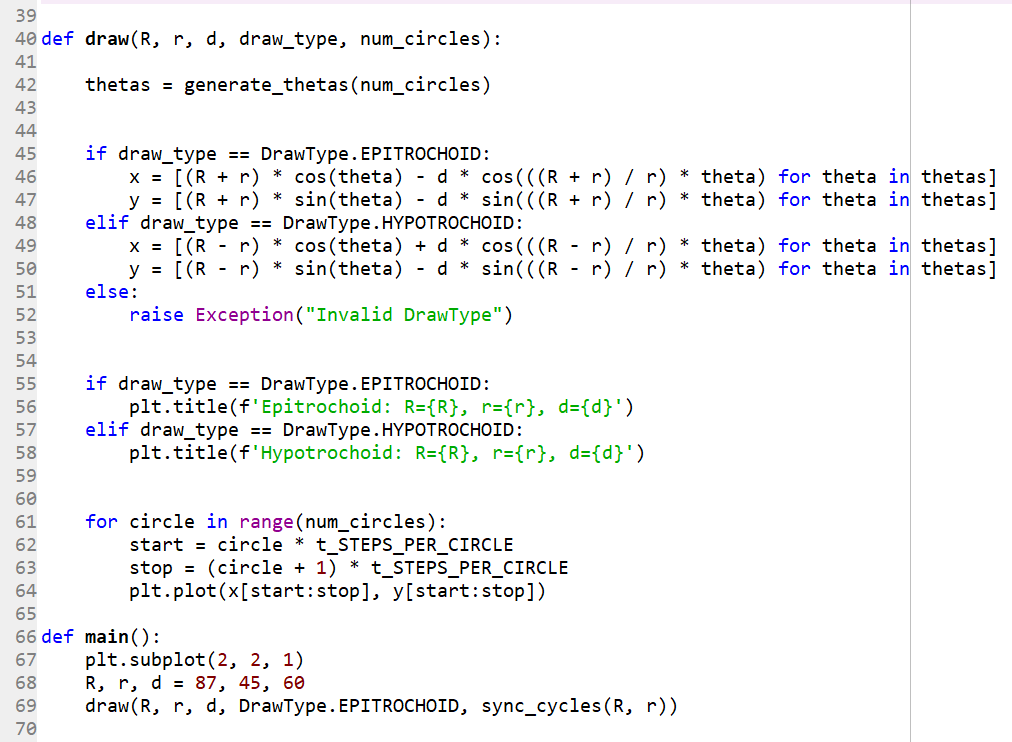
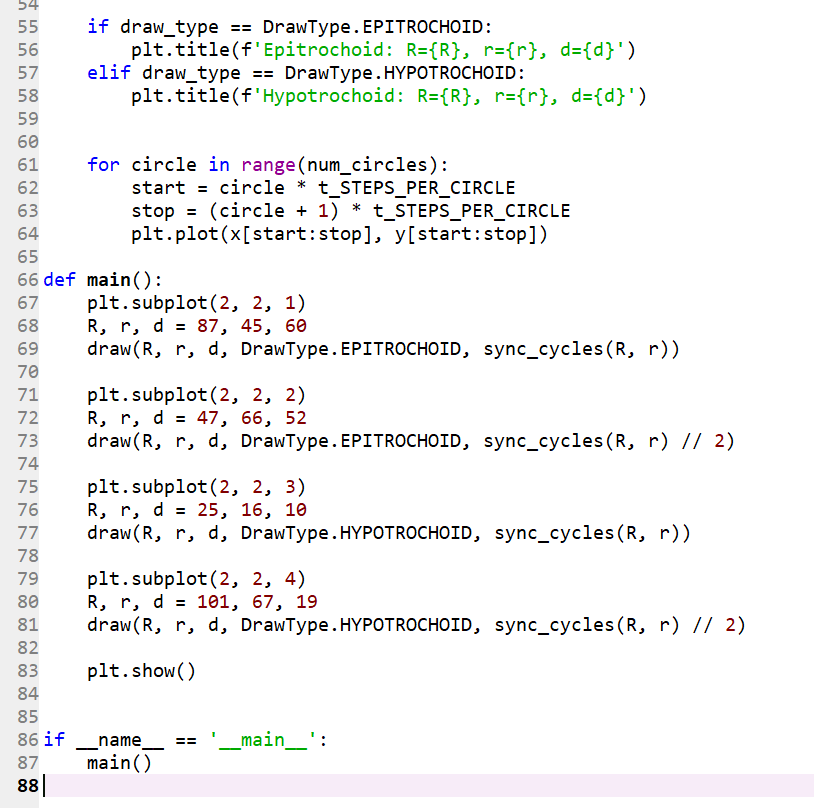
8 import matplotlib.pyplot as plt 9 from math import sin, cos, pi, ged 10 from enum import Enum 11 12 t_STEPS_PER_CIRCLE = 360 13 14 15 class DrawType (Enum): 16 EPITROCHOID = 1 17 HYPOTROCHOID = 2 18 19 20 def lcm(m, n): 21 return (m * n) // gcd(m, n) 22 23 24 def sync_cycles(R, r): 25 return lcm(R, r) // R 26 27 28 def generate_thetas(num_circles): 29 thetas = [(circle + (step / t_STEPS_PER_CIRCLE)) * 2 * pi for circle in range(num_circles) for step in range(t_STEPS_PER_CIRCLE)] thetas.append(num_circles * 2 * pi) return thetas 39 40 def draw(R, r, d, draw_type, num_circles): 41 thetas = generate_thetas(num_circles) Bg 46 if draw_type == DrawType. EPITROCHOID: x = [(R + r) * cos(theta) - d * cos(((R + r) / r) * theta) for theta in thetas] 39 40 def draw(R, r, d, draw_type, num_circles): 41 thetas = generate_thetas(num_circles) if draw_type == DrawType. EPITROCHOID: x = [(R + r) * cos(theta) - d * cos(((R + r) / r) * theta) for theta in thetas] y = [(R + r) * sin(theta) - d * sin(((R + r) / r) * theta) for theta in thetas] elif draw_type == DrawType.HYPOTROCHOID: x = [(R - r) * cos(theta) + d * cos(((R - r) / r) * theta) for theta in thetas] y = [(R - r) * sin(theta) - d * sin(((R - r) / r) * theta) for theta in thetas] else: raise Exception("Invalid DrawType") if draw_type == DrawType. EPITROCHOID: plt.title(f'Epitrochoid: R={R}, r={r}, d={d}') elif draw_type == DrawType. HYPOTROCHOID: plt.title(f'Hypotrochoid: R={R}, r={r}, d={d}') for circle in range(num_circles): start = circle * t_STEPS_PER_CIRCLE stop = (circle + 1) * t_STEPS_PER_CIRCLE plt.plot(x[start: stop], y[start: stop]) 64 65 67 66 def main(): plt. subplot(2, 2, 1) 68 R, r, d = 87, 45, 60 69 draw(R, r, d, DrawType. EPITROCHOID, sync_cycles(R, r)) 54 if draw_type == DrawType. EPITROCHOID: plt.title(f' Epitrochoid: R={R}, r={r}, d={d}') elif draw_type == DrawType.HYPOTROCHOID: plt.title(f'Hypotrochoid: R={R}, r={r}, d={d}') for circle in range(num_circles): 62 start = circle * t_STEPS_PER_CIRCLE stop = (circle + 1) * t_STEPS_PER_CIRCLE 64 plt.plot(x[start: stop], y[start: stop]) 65 66 def main(): 67 plt. subplot(2, 2, 1) 68 R, r, d = 87, 45, 60 69 draw(R, r, d, DrawType. EPITROCHOID, sync_cycles (R, r)) plt. subplot(2, 2, 2) R, r, d = 47, 66, 52 draw(R, r, d, DrawType. EPITROCHOID, sync_cycles(R, r) // 2) plt. subplot(2, 2, 3) R, r, d = 25, 16, 10 draw(R, r, d, DrawType. HYPOTROCHOID, sync_cycles (R, r)) 78 pit. subplot(2, 2, 4) R, r, d = 101, 67, 19 draw(R, r, d, DrawType. HYPOTROCHOID, sync_cycles (R, r) // 2) plt.show() 84 85 86 if _name_ == '_main_': 87 main() 88| 8 import matplotlib.pyplot as plt 9 from math import sin, cos, pi, ged 10 from enum import Enum 11 12 t_STEPS_PER_CIRCLE = 360 13 14 15 class DrawType (Enum): 16 EPITROCHOID = 1 17 HYPOTROCHOID = 2 18 19 20 def lcm(m, n): 21 return (m * n) // gcd(m, n) 22 23 24 def sync_cycles(R, r): 25 return lcm(R, r) // R 26 27 28 def generate_thetas(num_circles): 29 thetas = [(circle + (step / t_STEPS_PER_CIRCLE)) * 2 * pi for circle in range(num_circles) for step in range(t_STEPS_PER_CIRCLE)] thetas.append(num_circles * 2 * pi) return thetas 39 40 def draw(R, r, d, draw_type, num_circles): 41 thetas = generate_thetas(num_circles) Bg 46 if draw_type == DrawType. EPITROCHOID: x = [(R + r) * cos(theta) - d * cos(((R + r) / r) * theta) for theta in thetas] 39 40 def draw(R, r, d, draw_type, num_circles): 41 thetas = generate_thetas(num_circles) if draw_type == DrawType. EPITROCHOID: x = [(R + r) * cos(theta) - d * cos(((R + r) / r) * theta) for theta in thetas] y = [(R + r) * sin(theta) - d * sin(((R + r) / r) * theta) for theta in thetas] elif draw_type == DrawType.HYPOTROCHOID: x = [(R - r) * cos(theta) + d * cos(((R - r) / r) * theta) for theta in thetas] y = [(R - r) * sin(theta) - d * sin(((R - r) / r) * theta) for theta in thetas] else: raise Exception("Invalid DrawType") if draw_type == DrawType. EPITROCHOID: plt.title(f'Epitrochoid: R={R}, r={r}, d={d}') elif draw_type == DrawType. HYPOTROCHOID: plt.title(f'Hypotrochoid: R={R}, r={r}, d={d}') for circle in range(num_circles): start = circle * t_STEPS_PER_CIRCLE stop = (circle + 1) * t_STEPS_PER_CIRCLE plt.plot(x[start: stop], y[start: stop]) 64 65 67 66 def main(): plt. subplot(2, 2, 1) 68 R, r, d = 87, 45, 60 69 draw(R, r, d, DrawType. EPITROCHOID, sync_cycles(R, r)) 54 if draw_type == DrawType. EPITROCHOID: plt.title(f' Epitrochoid: R={R}, r={r}, d={d}') elif draw_type == DrawType.HYPOTROCHOID: plt.title(f'Hypotrochoid: R={R}, r={r}, d={d}') for circle in range(num_circles): 62 start = circle * t_STEPS_PER_CIRCLE stop = (circle + 1) * t_STEPS_PER_CIRCLE 64 plt.plot(x[start: stop], y[start: stop]) 65 66 def main(): 67 plt. subplot(2, 2, 1) 68 R, r, d = 87, 45, 60 69 draw(R, r, d, DrawType. EPITROCHOID, sync_cycles (R, r)) plt. subplot(2, 2, 2) R, r, d = 47, 66, 52 draw(R, r, d, DrawType. EPITROCHOID, sync_cycles(R, r) // 2) plt. subplot(2, 2, 3) R, r, d = 25, 16, 10 draw(R, r, d, DrawType. HYPOTROCHOID, sync_cycles (R, r)) 78 pit. subplot(2, 2, 4) R, r, d = 101, 67, 19 draw(R, r, d, DrawType. HYPOTROCHOID, sync_cycles (R, r) // 2) plt.show() 84 85 86 if _name_ == '_main_': 87 main() 88|