Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Make Graph and table and some calcultion (A)=K(A^nlog(A)=logK+nlog(A1 (3) time requised for 5:5 (3) effect +3 toss on Xacrall? ? {1=KV(C02FA0+akVCA022=kCA0 (A)=K(A^nlog(A)=logK+nlog(A1 CCOD=CBMFfor(CBMFCAMF(1)00=(AMF,(BMF)CAMF The concentration
Make Graph and table and some calcultion 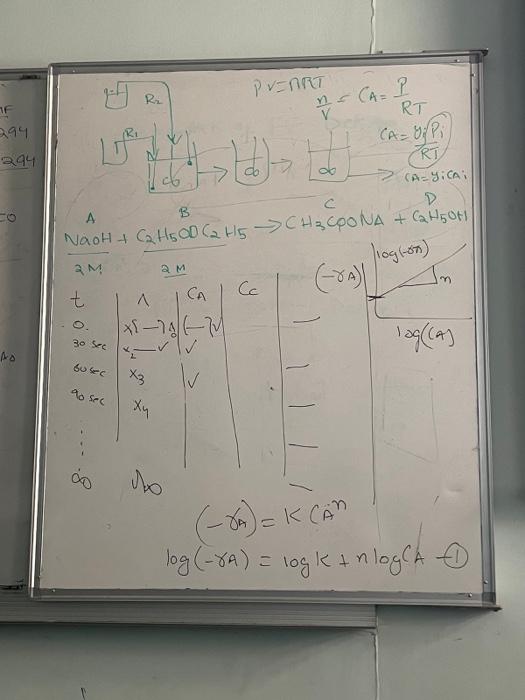



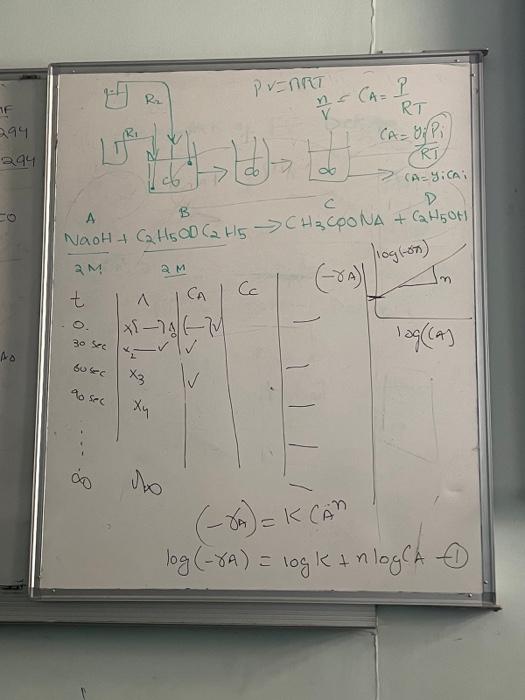



Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


